In diesem Kapitel werden Prüfungsaufgaben aus folgenden Gebieten vorgestellt und ausführlich besprochen. Die Theorie dazu müsste aus dem Lehrgang für Klasse E bekannt sein. Jedoch werden für Klasse A mehr Berechnungen verlangt.

In diesem Kapitel geht es um Kondensator, Spule und Transformator.

• Die Kapazität des Kondensators
• Kondensator im Gleichstromkreis
• Wechselstromwiderstand des Kondensators
• Phasenbeziehung beim Kondensator
• Der Verlustfaktor beim Kondensator
• Kondensatorschaltungen
• Die Spule
• Wechselstromwiderstand der Spule
• Phasenbeziehung bei der Spule
• Der Verluste der Spule
• Spulenschaltungen
• R-L-C Schaltungen
• Der Transformator
• Der Baluntransformator

Die Kapazität des Kondensators

Alle folgenden Aufgaben lassen sich mit den Theoriekenntnissen aus dem Amateurfunklehrgang Klasse E beantworten. Deshalb werden zu den einzelnen Aufgaben meistens nur kurze Tipps gegeben, ohne den Stoff aus dem Buch Klasse E zu wiederholen. Die Formel für die Kapazität eines Kondensators steht in der Formelsammlung der BNetzA mit \[ \boxed{ C = \varepsilon_0 \cdot \varepsilon_r \cdot \frac{A}{d} } \] Aus dieser Formel erkennt man, dass die Kapazität umgekehrt proportional ist zum Plattenabstand d. Umgekehrt proportional heißt: Wenn die eine Größe steigt, sinkt die andere.

Prüfungsfrage

TC201  Welche Aussage zur Kapazität eines Plattenkondensators ist richtig?
	Je größer die angelegte Spannung ist, desto kleiner ist die Kapazität.
	Je größer der Plattenabstand ist, desto kleiner ist die Kapazität.
	Je größer die Plattenoberfläche ist, desto kleiner ist die Kapazität.
	Je größer die Dielektrizitätszahl ist, desto kleiner ist die Kapazität.

Lösungsweg (hier klicken zum Anzeigen):

Der Kondensator im Gleichstromkreis

Wird ein Kondensator an Gleichspannung angeschlossen, wird er aufgeladen. Hierzu soll ein Versuch gemacht werden.

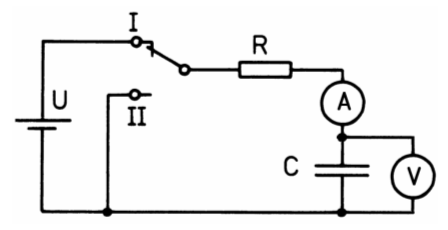
Zu Beginn des Ladevorgangs zeigt der Strommesser kurzzeitig einen großen Strom, der mit zunehmender Ladezeit abnimmt.

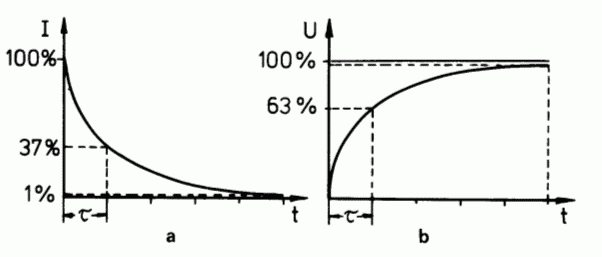
Die Ladezeit wird gekennzeichnet durch die so genannte Zeitkonstante τ (sprich: tau). In dieser Zeit steigt die Spannung auf 63 % der angelegten Ladespannung. Der Strom geht von seinem Anfangswert auf 37 % zurück.

Die Zeitkonstante ist abhängig von der Kapazität des Kondensators und vom Widerstand im Ladestromkreis.

\[ \boxed{\tau = R \cdot C} \qquad \Omega \cdot F = \frac{\text{V}}{\text{A}} \cdot \frac{\text{As}}{\text{V}} = \text{s} \]

τ (tau) ergibt sich in Sekunden, wenn man R in Ohm und C in Farad einsetzt.

Ähnlich verläuft der Vorgang beim Entladen , wenn man den Schalter in Bild 3-1 umlegt.

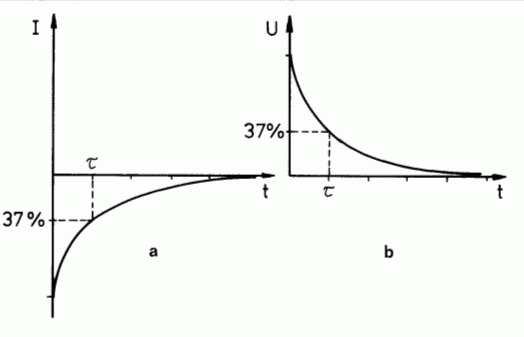
Der auf U voll aufgeladene Kondensator entlädt sich über den Widerstand R. Es fließt ein Strom in entgegen gesetzter Richtung (-I) durch das Messinstrument. Es dauert wieder eine Zeitkonstante τ bis der Strom von seinem Anfangswert auf 37 % abgesunken ist. Nach der gleichen Funktion verläuft die Spannung des Kondensators.

Prüfungsfrage

TC202  Welchen zeitlichen Verlauf hat die Spannung an einem entladenen Kondensator, wenn dieser über einen Widerstand an eine Gleichspannungsquelle angeschlossen wird?
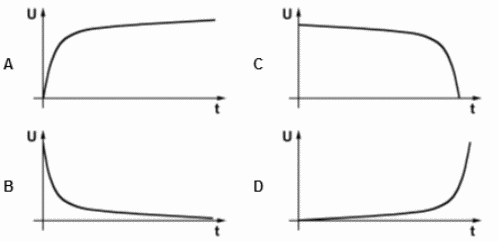	A
	B
	C
	D

Hinweis: Ein entladener Kondensator ist leer, die Spannung also null. Die Kurve U über t beginnt also bei Null. Außerdem steigt die Spannung erst schnell und dann langsam. Dies trifft für die Kurve A zu.

Der Wechselstromwiderstand des Kondensators

Bei ständig abwechselnder Ladung und Entladung (Rechteckwechselspannung) ergibt sich folgender Kurvenverlauf von Strom und Spannung (Bild 3-4).

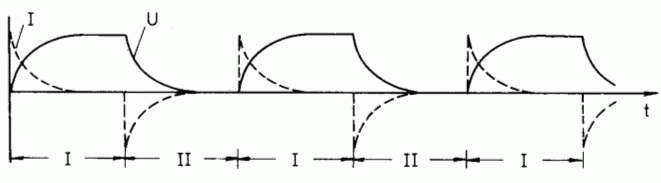
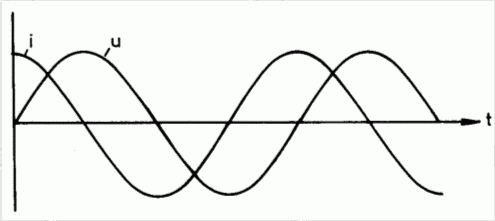
Schließt man einen Kondensator an sinusförmige Wechselspannung an, entspricht dies einer dauernden Umladung des Kondensators. Je schneller die Wechsel sind, desto rascher erfolgt die Umladung. Dabei zeigt ein Strommesser, der in den Stromkreis geschaltet ist, einen Wechselstrom an (Bild 3-5). Allerdings ist der Strom gegenüber der Spannung ähnlich verschoben, wie im Bild 3-4. Wenn die Spannung steigt, sinkt der Strom, und wenn die Spannung sinkt, steigt der Strom in negativer Richtung.

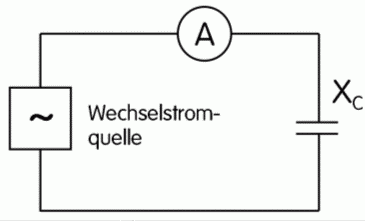
Wie beim „normalen“ Widerstand nach dem ohmschen Gesetz (man nennt ihn auch ohmschen Widerstand) bezeichnet man das Verhältnis aus anliegender Spannung zum fließenden Wechselstrom als Widerstand, hier bei Wechselstrom entsprechend Wechselstromwiderstand (X ) und bei einem Kondensator X_C.

\[ \boxed{ X_C = \frac{U_C}{I_C} } \]

Diese Formel wird für Prüfungsfrage TC207 noch benötigt. Wir benötigen für die Lösung dieser Prüfungsaufgabe noch eine Formel für den Wechselstromwiderstand eines Kondensators, wobei man X_C aus der Kapazität und der Frequenz berechnen kann.

Folgende Überlegungen dienen der Ableitung dieser Formel. Der Wechselstrom I_C ist umso größer, je größer die Kapazität des Kondensators ist und je häufiger die Umladung erfolgt. Dies entspricht der Frequenz. Außerdem ist der Strom natürlich auch proportional zu der angelegten Spannung. Setzt man als Frequenz die Kreisfrequenz ω = 2πf ein, erhält man den gesuchten Zusammenhang.

\[ I_C = \omega \cdot C \cdot U_C \]

Diese Gleichung wird etwas umgestellt und für \( \frac{U}{I} = X \) eingesetzt.

\[ \frac{1}{\omega \cdot C} = \frac{U_C}{I_C} = X_C \]

oder

\[ \boxed{ X_C = \frac{1}{\omega \cdot C} } \]

Mit dieser Formel lässt sich der Wechselstromwiderstand des Kondensators (auch kapazitiver Widerstand oder Blindwiderstand genannt) allein aus der Kapazität und der anliegenden Frequenz ω = 2 π f berechnen.

ω (omega) ist die Kreisfrequenz. Das ist die Umfangsgeschwindigkeit, mit der der Zeiger im Zeigerdiagramm (siehe Lektion 11: Signale) den Einheitskreis durchläuft.

Merken Sie sich also bitte

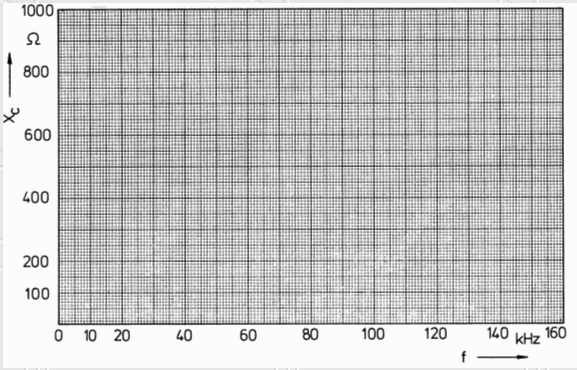
\[ \boxed{ \omega = 2 \cdot \pi \cdot f } \]

Um die Frequenzabhängigkeit grafisch aufzeigen zu können, soll der Wechselstromwiderstand eines Kondensators einmal in Abhängigkeit von der Frequenz berechnet werden.

ÜB03-1  Berechnen Sie den Wechselstromwiderstand eines Kondensators von 10 nF bei folgenden Frequenzen a) f = 15,9 kHz, b) f = 100 kHz, c) f = 159 kHz und tragen Sie die Werte in das Diagramm Bild 3-6 ein.

Lösungsweg (hier klicken zum Anzeigen):

Merke: Ein Kondensator stellt für Wechselstrom einen Widerstand dar, während er Gleichstrom sperrt.
Mit steigender Frequenz nimmt der Wechselstromwiderstand (kapazitiver Blindwiderstand) des Kondensators ab.

Prüfungsfrage

TC204  Wie verhält sich der Wechselstromwiderstand eines Kondensators mit zunehmender Frequenz?
	Er bleibt konstant.
	Er nimmt zu.
	Er nimmt ab.
	Er wird unendlich.

Prüfungsfrage

TC205  Wie groß ist der kapazitive Widerstand eines 10-pF-Kondensators bei 100 MHz?
	31,8 Ω
	159 Ω
	318 Ω
	1,59 kΩ

Lösungsweg (hier klicken zum Anzeigen):

Prüfungsfrage

TC206  An einem unbekannten Kondensator liegt eine Wechselspannung mit 16 V und 50 Hz. Es wird ein Strom von 32 mA gemessen. Welche Kapazität hat der Kondensator?
	0,45 µF
	0,637 µF
	4,5 µF
	6,37 µF

Lösungsweg (hier klicken zum Anzeigen):

Phase zwischen Strom und Spannung

Zwischen Strom und Spannung herrscht bei einem idealen Kondensator an Wechselspannung eine Phasenverschiebung von 90° (Bild 3-7). Und zwar eilt der Strom der angelegten Spannung vor. Dieses ist folgendermaßen erklärbar. Legt man an einen ungeladenen Kondensator (U_C = 0) eine Spannung an, fließt zunächst ein großer Ladestrom, dann steigt die Spannung am Kondensator und der Stromnimmt ab.

In der Elektrotechnik kann man diese Phasenverschiebung zwischen Strom und Spannung auch durch rotierende Zeiger darstellen (Zeigerdiagramm). In der Lektion 11 wird dieses Verfahren noch genauer erklärt. Die Zeiger rotieren links herum (entgegen dem Uhrzeigersinn). Der Nullpunkt ist die Richtung nach rechts. Für einen Kondensator sieht ein solches Zeigerdiagramm folgendermaßen aus (Bild 3-7 links). Man schreibt kleine Buchstaben für Spannung (u) und für Strom (i) an die Achsen, wodurch angedeutet werden soll, dass es sich um Wechselgrößen handelt.

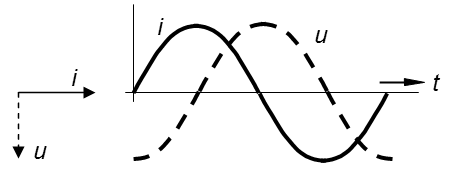
Eselsbrücke: Kondensator – Strom eilt vor.

Prüfungsfrage

TC203  Ein verlustloser Kondensator wird an eine Wechselspannungsquelle angeschlossen. Welche Phasenverschiebung zwischen Spannung und Strom stellt sich ein?
	Die Spannung eilt dem Strom um 45° voraus.
	Der Strom eilt der Spannung um 45° voraus.
	Der Strom eilt der Spannung um 90° voraus.
	Die Spannung eilt dem Strom um 90° voraus.

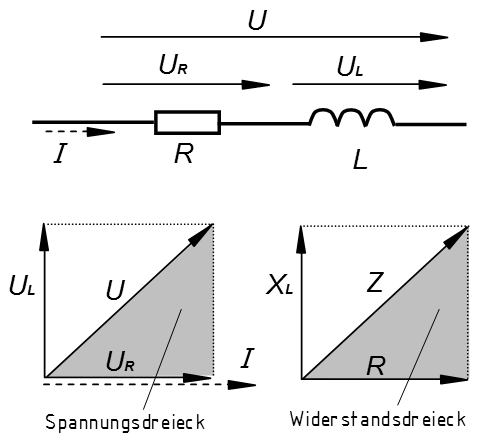
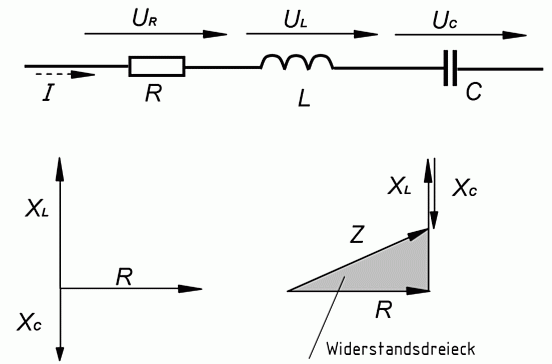
Kondensator und Widerstand in Reihenschaltung

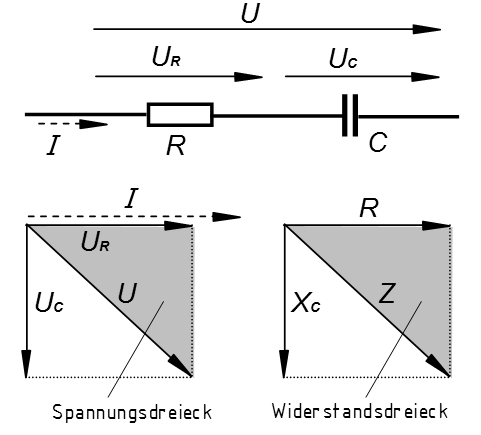
Bei der Reihenschaltung aus einem Wirkwiderstand (R) und einem idealen Kondensator eilt die Wechselspannung am Kondensator dem Strom um 90° nach (Bild 3-8). Die Spannung am Wirkwiderstand ist mit dem Strom in Phase. In den Zeigerbildern stehen die Zeiger der Wirkgrößen (Spannung an R) und der Blindgrößen (Spannung an C) senkrecht zueinander. Die Richtung nach unten wird in der "komplexen Rechnung" auch negative Richtung genannt.

Interessant ist, dass die Gesamtspannung U nicht die einfache arithmetische Summe aus U_R plus U_C ist. In der Wechselstromtechnik gilt die "geometrische" Addition (Bild 3-8): Man bekommt die Gesamtspannung dadurch, dass man die Diagonale zeichnet. Aus dem daraus entstehenden Spannungsdreieck kann man die Gesamtspannung berechnen, denn im rechtwinkligen Dreieck gilt a²+ b²= c². Auf das Spannungsdreieck angewendet ergibt es

\[ U^2 = {U_R}^2 + {U_C}^2 \quad \text{oder} \quad U = \sqrt{{U_R}^2 + {U_C}^2} \]

Dividiert man die Spannungen durch den gemeinsamen Strom, erhält man die Widerstände. Daraus ergibt sich das Widerstandsdreieck. Den Gesamtwiderstand nennt man Scheinwiderstand Z. Auch hier gilt

\[ Z = \sqrt{R^2 + {X_C}^2} \]

Beispiel
Ein Wirkwiderstand von 100 Ω und ein Kondensator von 10 nF sind in Reihe an eine Sinusspannung von 159 kHz angeschlossen. Wie groß ist der Scheinwiderstand Z der Reihenschaltung?

Zunächst wird der kapazitive Blindwiderstand X_C ausgerechnet. Es sind die Werte aus der Übungsaufgabe zum Diagramm 3-6. Dort wurde für X_C = 100 Ω berechnet. Die Reihenschaltung von R und X_C beträgt nun nicht etwa 200 Ω, sondern wird nach folgender Formel berechnet.

\[ \begin{align} Z& = \sqrt{R^2 + {X_C}^2} \\ Z& = \sqrt{100^2 + 100^2}\ \Omega = \mathbf{141 \ \Omega} \end{align} \]

Zu diesem Thema gibt es keine Rechenaufgabe bei den Prüfungsaufgaben. Folgende Aufgabe könnte man dazu rechnen.

Prüfungsfrage

TC207  Was versteht man unter dem Blindwiderstand eines Kondensators und von welchen physikalischen Größen hängt er ab?
	Der Blindwiderstand ist der Wechselstromwiderstand eines Kondensators. Er ist abhängig von der Kapazität des Kondensators und der anliegenden Frequenz. Im Blindwiderstand entstehen keine Wärmeverluste.
	Der Blindwiderstand ist der Gleichstromwiderstand eines Kondensators. Er ist abhängig vom Isolationsmaterial des Kondensators und der anliegenden Spannung. Auch im Blindwiderstand entstehen Wärmeverluste.
	Der Blindwiderstand ist der Wechselstromwiderstand eines Kondensators. Er ist abhängig von der Blindkapazität des Kondensators und der anliegenden Spannung. Im Blindwiderstand entstehen hohe Verluste.
	Der Blindwiderstand ist der HF-Gleichstromwiderstand eines Kondensators. Er wird mit steigender Kapazität sowie bei erhöhtem Wechselstromanteil und steigender Frequenz größer. Je höher die Frequenz umso eher wandern die Ladungen an die Plattenränder (Skin-Effekt).

Hinweis: Siehe Bild 3-8! Nach unten ist der negative Bereich.

Verluste beim Kondensator

Liegt eine Wechselspannung am Kondensator, wird ein kleiner Teil der zur Elektronenverschiebung im Dielektrikum geleisteten Arbeit in Verlustwärme umgesetzt. Die Stärke der Wärmeentwicklung ist vom Material und von der Frequenz der angelegten Wechselspannung abhängig. Man stellt sich vor, dass die Verlustwärme durch den Strom eines parallel geschalteten Widerstandes R_V hervorgerufen wird. Deshalb verwendet man folgendes Ersatzbild (Bild 3-9) für einen „realen“ Kondensator mit Verlusten.

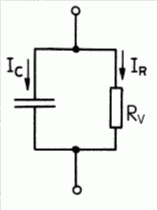
Das Verhältnis des Wechselstroms I_R durch diesen Widerstand zum Strom I_C durch den Kondensator bezeichnet man als Verlustfaktor tan δ (sprich: tangens delta).

\[ \tan\delta = \frac{I_R}{I_C} = \frac{X_C}{R_V} \]

Den Kehrwert davon nennt man übrigens den Gütefaktor eines Kondensators. Je größer der parallele Verlustwiderstand ist, desto höher ist die Güte des Kondensators.

Für einige typische Kondensatoren finden Sie den Verlustfaktor (Diagramm Bild 10) aufgetragen.

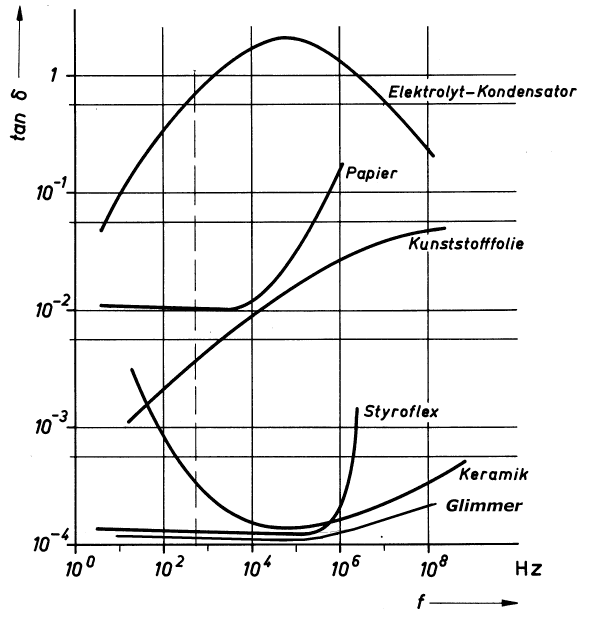
Für die Anwendung im Hochfrequenzbereich sollte ein Kondensator nach diesem Verlustfaktor ausgewählt werden. Ein kleiner Wert steht für einen geringen Verlustfaktor. Aus dem Diagramm erkennt man: Glimmer-, Keramik- und Styroflexkondensatoren sind die besten Kondensatoren für den MHz-Bereich.

Prüfungsfrage

TC208  Neben dem kapazitiven Blindwiderstand treten im Wechselstrom durchflossenen Kondensator auch Verluste auf, die rechnerisch in einem parallelgeschalteten Verlustwiderstand zusammengefasst werden können. Die Kondensatorverluste werden angegeben durch
	den relativen Verlustwiderstand in Ohm pro Picofarad, mit dem die Kondensatorgüte berechnet werden kann.
	den relativen Blindwiderstand in Ohm pro Picofarad, mit dem die Kondensatorgüte berechnet werden kann.
	den Verlustfaktor tan δ (Tangens Delta), der dem Kehrwert des Gütefaktors entspricht.
	den Verlustfaktor cos φ (Cosinus Phi), der dem Kehrwert des Gütefaktors entspricht.

Parallelschaltung von Kondensatoren

Im Lehrbuch zur Klasse E, Lektion 5 wurden bereits die Parallelschaltung und die Reihenschaltung von Kondensatoren behandelt. Bei der Parallelschaltung werden die Kapazitäten der einzelnen Kondensatoren einfach addiert. Allerdings muss man bei der Prüfung aufpassen, ob denn die zu addierenden Kondensatoren die gleiche Einheit haben.

Prüfungsfrage

TD116  Welche Gesamtkapazität ergibt sich bei einer Parallelschaltung der Kondensatoren 0,1 μF, 150 nF und 50000 pF?
	0,027 μF
	0,255 μF
	0,3 μF
	2,73 nF

Lösungsweg (hier klicken zum Anzeigen):

Prüfungsfrage

TD103  Wie groß ist die Gesamtkapazität von drei parallel geschalteten Kondensatoren von 20 nF, 0,03 µF und 15000 pF?
	0,650 µF
	650 nF
	0,065 µF
	650 000 pF

Lösungsweg (hier klicken zum Anzeigen):

Prüfungsfrage

TD120  Wie groß ist die Gesamtkapazität dieser Schaltung, wenn C1  = 0,1 nF, C2  = 1,5 nF, C3  = 220 pF und die Eigenkapazität der Spule 1 pF beträgt?
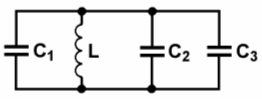	66 pF
	1,6 pF
	1821 pF
	≈ 1 pF

Lösungsweg (hier klicken zum Anzeigen):

Reihenschaltung von Kondensatoren

Bei der Reihenschaltung von Kondensatoren gilt eine Formel, die wie die Formel der Parallelschaltung von Widerständen aussieht. Sie finden folgende Formel auch in der Formelsammlung der BNetzA.

\[ \boxed{\frac{1}{C} = \frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}+\cdots} \]

Für zwei Kondensatoren in Reihenschaltung kann man die Formel natürlich einfach nach C₂ abbrechen, aber es gibt auch eine umgestellte Formel.

\[ \boxed{{C} = \frac{C_1 \cdot C_2}{C_1 + C_2}} \]

Auch für drei Kondensatoren lässt sich die Formel nach C umstellen und man erhält eine ziemlich kompliziert aussehende Formel zur Berechnung der Gesamtkapazität von drei in Reihe geschalteten Kondensatoren. Sie lautet:

\[ \boxed{{C} = \frac{C_1 \cdot C_2 \cdot C_3}{C_1 \cdot C_2 + C_1 \cdot C_3 + C_2 \cdot C_3}} \]

Prüfungsfrage

TD117  Welche Gesamtkapazität ergibt sich bei einer Reihenschaltung der Kondensatoren 0,1 µF, 150 nF und 50000 pF?
	0,255 µF
	0,027 µF
	0,3 µF
	2,73 nF

Lösungsweg (hier klicken zum Anzeigen):

Prüfungsfrage

TD106  Wie groß ist die Gesamtkapazität, wenn drei Kondensatoren C1  = 0,06 nF, C2  = 40 pF und C3  = 20 pF in Reihe geschaltet werden?
	10,9 pF
	0,12 nF
	4,1 pF
	40 pF

Lösungsweg (hier klicken zum Anzeigen):

Prüfungsfrage

TD102  Eine Reihenschaltung besteht aus drei Kondensatoren von je 0,03 µF. Wie groß ist die Gesamtkapazität dieser Schaltung?
	0,09 µF
	0,01 µF
	0,001 µF
	0,009 µF

Lösungsweg (hier klicken zum Anzeigen):

Gemischte Schaltung von Kondensatoren

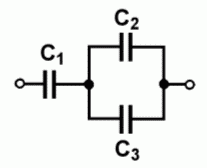
Bei gemischten Schaltungen von parallel und in Reihe geschalteten Kondensatoren gehen Sie so vor, wie Sie es bei den Widerständen gelernt haben. Schauen Sie zunächst, welche Kondensatoren eindeutig parallel oder in Reihe geschaltet sind, berechnen die Ersatzkapazität und vereinfachen die Schaltung so lange, bis nur noch eine einzige Ersatzkapazität übrig bleibt.

Prüfungsfrage

TD118  Welche Gesamtkapazität hat die Schaltung von Kondensatoren nach Bild 3-11, wenn C1  = 0,01 µF, C2  = 5 nF und C3  = 5000 pF betragen?
	0,015 nF
	5 nF
	7,5 nF
	12,5 nF

Lösungsweg (hier klicken zum Anzeigen):

Prüfungsfrage

TD119  Welche Gesamtkapazität hat die Schaltung nach Bild 3-11, wenn C1 = 2 µF, C2 = 1 µF und C3 = 1 µF betragen?
	1,0 µF
	4400 nF
	2,5 µF
	4,0 µF

Lösungsweg (hier klicken zum Anzeigen):

Die Spule

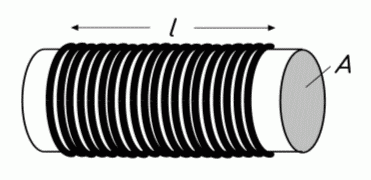
Im Kapitel 6 des Amateurfunklehrgangs für Klasse E wird bereits erläutert, dass eine Spule im Prinzip aus aufgewickeltem Draht besteht. Aus der Anzahl der Windungen dieser Drahtwicklung und den Eigenschaften des Wickelkerns kann man die Induktivität einer Spule berechnen. µ₀ ist die "Permeabilität des luftleeren Raums" (ein Umrechnungsfaktor) und µ_r ist die relative Permeabilität die angibt, wieviel mal stärker das Magnetfeld durch das Kernmaterial wird. Diese Faktoren sind vergleichbar mit ε₀ und ε_r beim Kondensator.

\[ \boxed{L = \frac{\mu_0 \cdot \mu_r \cdot A \cdot N^2}{l_m}} \quad \text{mit} \quad \mu_0 = 1,2566\cdot10^{-6} \frac{\text{Vs}}{\text{Am}} \]

Aus dieser Formel erkennt man, dass die Induktivität L von der Querschnittsfläche A proportional, von der Windungszahl N quadratisch proportional und von der Länge der Zylinderspule l_m umgekehrt proportional abhängig ist. Wickelt man eine „dickere“ Spule (größerer Durchmesser, nicht dickerer Draht), wird die Fläche größer und damit gleichzeitig die Induktivität. Verdoppelt man die Windungszahl, wird die Induktivität viermal (2² = 4) so groß. Erhöht man die Länge der Spule bei gleicher Windungszahl, indem man die Windungen spreizt, wird die Induktivität kleiner. Umgekehrt: Staucht man die Spule, so dass die Länge der Spule geringer wird, erhöht sich die Induktivität. Dazu gibt es eine Prüfungsfrage.

Prüfungsfrage

TC309  Wie kann man die Induktivität einer Spule vergrößern?
	Durch Stauchen der Spule (Verkürzen der Spulenlänge).
	Durch Auseinanderziehen der Spule (Vergrößerung der Spulenlänge).
	Durch Einführen eines Kupferkerns in die Spule.
	Durch Einbau der Spule in einen Abschirmbecher.

Lösungsweg (hier klicken zum Anzeigen):

Für Kerne mit bekannten Abmessungen oder auch für Wickelkörper geben die Hersteller direkt einen Kernfaktor an, den man A_L -Wert nennt. Der A_L -Wert ist ein Teil aus obiger Formel, nämlich der Faktor des Bruches ohne die Windungszahl.

\[ \begin{align} L& = \frac{\mu_0 \cdot \mu_r \cdot A}{l_m} \cdot N^2 \\ \\ A_L& = \frac{\mu_0 \cdot \mu_r \cdot A}{l_m} \end{align} \]

Dann vereinfacht sich die Formel erheblich zu

\[ \boxed{L = A_L \cdot N^2} \]

Diese Formel steht ebenfalls in der Formelsammlung der BNetzA. Dort ist vermerkt, dass ein A_L -Wert immer in nH (Nanohenry) angegeben wird.

Prüfungsfrage

TC310  Mit einem Schalenkern, dessen AL -Wert mit 250 angegeben ist, soll eine Spule mit einer Induktivität von 2 mH hergestellt werden. Wie groß ist die erforderliche Windungszahl?
	3
	53
	89
	2828

Lösungsweg (hier klicken zum Anzeigen):

Prüfungsfrage

TC311  Wie groß ist die Induktivität einer Spule mit 300 Windungen, die auf einen Kern mit einem AL -Wert von 1250 gewickelt ist?
	112,5 mH
	112,5 μH
	11,25 mH
	1,125 mH

Lösungsweg (hier klicken zum Anzeigen):

Prüfungsfrage

TC312  Wie groß ist die Induktivität einer Spule mit 14 Windungen, die auf einen Kern mit einem AL -Wert von 1,5 gewickelt ist?
	2,94 μH
	0,294 μH
	29,4 nH
	2,94 nH

Prüfungsfrage

TC313  Ein Kernmaterial hat einen AL -Wert von 30. Wie groß ist die erforderliche Windungszahl zur Herstellung einer Induktivität von 12 μH?
	360
	400
	20
	6

Lösungsweg (hier klicken zum Anzeigen):

Spule an Gleichspannung

Im Amateurfunklehrgang für die Klasse E wurde unter der Überschrift „Induktivität“ erklärt, dass beim Anlegen einer Gleichspannung über einen Schalter der Strom durch die Spule verzögert wird. Es wurde dort ein Versuch zur Demonstration der Selbstinduktion gezeigt. Zusammengefasst: Es bildet sich eine Gegenspannung, die dem Strom entgegen wirkt. Die Spannung ist also sofort da, fällt dann aber zügig und dann immer langsamer werdend (nach einer e-Funktion) ab.

Prüfungsfrage

TC301  An eine Spule wird über einen Widerstand eine Gleichspannung angelegt. Welches der nachfolgenden Diagramme zeigt den zeitlichen Verlauf der Spannung über der Spule?

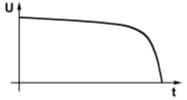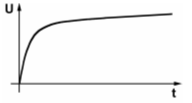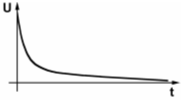Prüfungsfrage

TC304  Beim Anlegen einer Gleichspannung U = 1 V an eine Spule messen Sie einen Strom. Wird der Strom beim Anlegen von einer Wechselspannung mit Ueff  = 1 V größer oder kleiner?
	Beim Betrieb mit Gleichspannung wirkt nur der Gleichstromwiderstand der Spule. Beim Betrieb mit Wechselspannung wirkt nur der kleinere induktive Widerstand XL. Der Strom wird größer.
	Beim Betrieb mit Gleich- oder Wechselspannung wirkt nur der ohmsche Widerstand XL der Spule. Der Strom bleibt gleich.
	Beim Betrieb mit Gleichspannung wirkt nur der Gleichstromwiderstand der Spule. Beim Betrieb mit Wechselspannung wird der induktive Widerstand XL wirksam und erhöht den Gesamtwiderstand. Der Strom wird kleiner.
	Beim Betrieb mit Wechselspannung wirkt nur der Wechselstromwiderstand der Spule. Beim Betrieb mit Gleichspannung wird nur der ohmsche Widerstand XL wirksam. Der Strom wird größer.

Der Wechselstromwiderstand der Spule

Ebenfalls im Buch für Klasse E wurde der Wechselstromwiderstand der Spule ohne Berücksichtigung der Verluste der Blindwiderstand erklärt. Ähnlich wie beim Kondensator gilt

\[ X_L = \frac{U_L}{I_L} \text{ oder } X_L = \omega \cdot L \]

U geteilt durch I ist wie R beim ohmschen Gesetz. Allerdings muss für Zusammenschaltungen bei der Berechnung ein Phasenwinkel berücksichtigt werden.

Prüfungsfrage

TC306    Was versteht man unter dem Blindwiderstand einer Spule und von welchen physikalischen Größen hängt er ab?
	Der Blindwiderstand ist der Wechselstromwiderstand einer Spule. Er ist abhängig von der Induktivität der Spule und der anliegenden Frequenz. Im Blindwiderstand entstehen keine Wärmeverluste.
	Der Blindwiderstand ist der Gleichstromwiderstand einer Spule. Er ist abhängig vom Isolationsmaterial der Spule und der anliegenden Spannung. Auch im Blindwiderstand entstehen Wärmeverluste.
	Der Blindwiderstand ist der Wechselstromwiderstand einer Spule. Er ist abhängig von der Blindinduktivität der Spule und der anliegenden Spannung. Im Blindwiderstand entstehen hohe Verluste.
	Der Blindwiderstand ist der HF-Gleichstromwiderstand einer Spule. Er wird mit steigender Induktivität sowie bei erhöhtem Wechselstromanteil und steigender Frequenz größer. Je tiefer die Frequenz umso eher wandern die Elektronen an den Spulenrand (Skin-Effekt).

Prüfungsfrage

TC305    Wie groß ist der Wechselstromwiderstand einer Spule mit 3 µH Induktivität bei einer Frequenz von 100 MHz?
	1,9 Ω
	942 Ω
	1885 Ω
	1885 kΩ

Lösungsweg (hier klicken zum Anzeigen):

Um die Frequenzabhängigkeit zu verdeutlichen, lösen Sie folgende Übungsaufgabe.

Übungsaufgabe

ÜB03-2  Berechnen Sie den Wechselstromwiderstand einer Drosselspule von 1 Henry bei den Frequenzen 50 Hz, 100 Hz, 500 Hz und 1000 Hz. Die Verluste werden nicht berücksichtigt.Tragen Sie anschließend die Ergebnisse in folgendes Diagramm ein und verbinden Sie die Punkte.

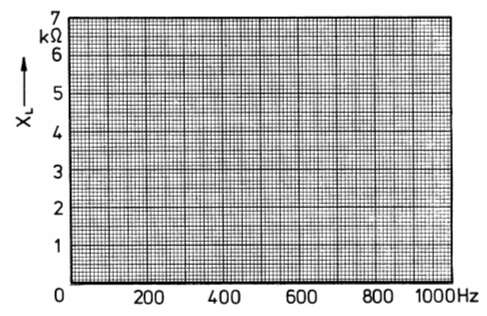
Prüfungsfrage

TC303  Wie verhält sich der Wechselstromwiderstand einer Spule mit zunehmender Frequenz?
	Er nimmt zu.
	Er nimmt ab.
	Er bleibt konstant.
	Er steigt auf ein Maximum und fällt dann ab.

Lösungsweg (hier klicken zum Anzeigen):

Phase zwischen Strom und Spannung bei einer Spule

Zwischen Strom und Spannung herrscht bei einer idealen Spule an Wechselspannung eine Phasenverschiebung von 90°. Und zwar eilt der Strom der Spannung nach. Vergleichen Sie bitte einmal die Bilder 3-15 und 3-7! Im Zeigerdiagramm der Spule zeigt u nach oben in den positiven Bereich. Die Zeiger drehen sich links herum (entgegen dem Uhrzeiger). Der Stromzeiger i eilt also dem Spannungszeiger u um 90° nach. Beim Kondensator zeigt u nach unten.

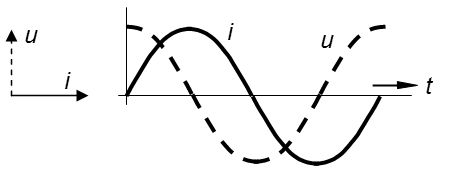
Der Strom eilt der Spannung nach. Dies ist folgendermaßen erklärbar. Nach dem Anlegen einer Spannung an eine Spule wird zunächst durch Selbstinduktion eine Gegenspannung erzeugt, die den Stromfluss verhindert. Erst nach einer gewissen Zeit beginnt der Strom zu fließen (siehe auch Versuch zur Induktivität im Amateurfunklehrgang Klasse E).

Eselsbrücken im Vergleich:
Induktivität– Strom zu spät.
Kondensator– Strom eilt vor.

Prüfungsfrage

TC302  In einer reinen Induktivität, die an einer Wechselspannungsquelle angeschlossen ist, eilt der Strom der angelegten Spannung ...
	um 90° voraus.
	um 90° nach.
	um 45° voraus.
	um 45° nach.

Lösungsweg (hier klicken zum Anzeigen):

Die Verluste der Spule

Die Verluste einer Spule äußern sich wie ein Serienwiderstand. Bei der Berechnung des Blindwiderstandes tun wir so, als ob die Spule aus Draht mit null Ohm besteht. Aber jede Kupferwicklung stellt natürlich einen Drahtwiderstand dar, wenn er auch gegenüber dem Wechselstromwiderstand der Spule klein ist. Eine Spule hat eine umso höhere Güte Q, je geringer der Gleichstromwiderstand R_s im Verhältnis zum Wechselstromwiderstand ist. Dies kann man in einer Formel ausdrücken.

\[ \boxed{Q = \frac{X_L}{R_s}} \quad \boxed{\tan \delta = \frac{R_s}{X_L}} \]

Manchmal wird die Güte Q wie beim Kondensator auch als Verlustfaktor tan δ angegeben. Dies ist der Kehrwert der Güte. Die Formeln finden Sie in der Formelsammlung der BNetzA unter Schwingkreis.

Prüfungsfrage

TC307    Neben dem induktiven Blindwiderstand treten in der Wechselstrom durchflossenen Spule auch Verluste auf, die rechnerisch in einem seriellen Verlustwiderstand zusammengefasst werden können. Die Verluste einer Spule werden angegeben durch
	den relativen Verlustwiderstand in Ohm pro Nanohenry, mit dem die Spulengüte berechnet werden kann.
	den relativen Blindwiderstand in Ohm pro Nanohenry, mit dem die Spulengüte berechnet werden kann.
	den Verlustfaktor tan δ (Tangens Delta), der dem Kehrwert des Gütefaktors entspricht.
	den Verlustfaktor cos φ (Cosinus Phi), der dem Kehrwert des Gütefaktors entspricht.

Lösungsweg (hier klicken zum Anzeigen):

Der Vollständigkeit halber sollen auch hier wieder wie beim Kondensator die Zeigerdreiecke für die Reihenschaltung von Spule und Wirkwiderstand angegeben werden.

Anwendungen der Spule

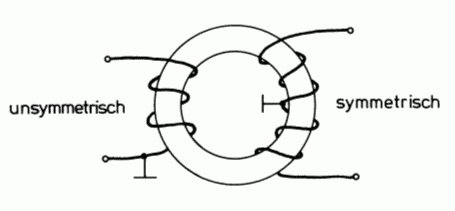
Für die Spule gibt es vielfältige Anwendungen im Amateurfunk. Für die Hochfrequenzentstörung benutzt man Ringkerne aus Ferritmaterial, durch die das Netzkabel mehrfach durchgezogen wird. Zur Antennenanpassung verwendet man solche Ringkerne, um Wicklungen für ein Symmetrierglied (Balun, siehe Lektion 10) herzustellen.

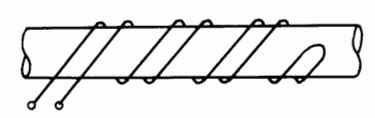
Für die Unterdrückung von „parasitären“ Schwingungen kann man eine Breitband-Anodendrossel dadurch herstellen, dass man etwas Kupferdraht auf einen niederohmigen Widerstand wickelt.

Zur Anpassung von Antennen verwendet man L-C-Schaltungen mit riesigen Luftspulen.

Prüfungsfrage

TC317  Für die Unterdrückung parasitärer Schwingungen kann eine verlustbehaftete Drosselspule verwendet werden. Wie wird eine solche Spule gebaut?
	Die Spule wird um einen Widerstand mit niedrigem Widerstandswert gewickelt.
	Es wird eine freitragende Spule aus dickem Kupferdraht, der mit einem Silberbelag versehen ist, hergestellt.
	Es wird ein dicker Kupferdraht um einen Widerstand mit sehr hohem Widerstandswert gewickelt.
	Es wird ein Kohleschichtwiderstand mit niedrigem Widerstandswert verwendet.

Prüfungsfrage

TC316  Das nebenstehende Bild zeigt einen Kern, um den ein Kabel für den Bau einer Netzdrossel gewickelt ist. Der Kern sollte aus ...
	Kunststoff bestehen.
	Ferrit bestehen.
	Stahl bestehen.
	paramagnetischem Material bestehen.

Lösungsweg (hier klicken zum Anzeigen):

Prüfungsfrage

TC319  Durch Gegeninduktion wird in einer Spule eine Spannung erzeugt, wenn ...
	veränderlicher Strom durch eine magnetisch gekoppelte benachbarte Spule fließt.
	durch eine magnetisch gekoppelte benachbarte Spule kein Strom fließt.
	ein Magnet in die Spule eingeführt oder wieder aus ihr entfernt wird.
	sich die Spule in einem konstanten Magnetfeld befindet.

Bei Messwiderständen hoher Leistung stört die Induktivität. Deshalb wickelt man so, dass zur Hälfte im entgegen­gesetzten Sinn gewickelt wird (Bild 3-19).

Jedes Stückchen Draht, jeder Leiter, ob er gerade oder kreisförmig verläuft (Bild 3-20), erzeugt beim Stromfluss ein magnetisches Feld. Umgekehrt schließt man daraus: Jeder Leiter hat eine gewisse Induktivität. Deshalb muss man besonders bei elektronischen Geräten für ultrahohe Frequenzen (UHF) die Leitungsverbindungen sehr kurz halten.

Prüfungsfrage

TC308  Hat ein gerades Leiterstück eine Induktivität?
	Ja, jeder Leiter, gleich welche Form er hat, weist eine Induktivität auf.
	Nein, der Leiter muss wenigstens eine Krümmung (eine viertel, halbe oder ganze Windung) aufweisen.
	Ja, aber die Größe der Induktivität hängt vom spezifischen Widerstand des Leitermaterials ab.
	Ja, aber nicht immer, denn abgeschirmte Leiter, beispielsweise Koaxialkabel und Streifenleitungen, weisen nur eine Kapazität auf.

Das in der Spule erzeugte Magnetfeld kann gelegentlich störend wirken. Denn durch Gegeninduktion kann in einer benachbarten Spule eine Spannung erzeugt werden. Deshalb werden solche Spulen oft durch Abschirmbecher aus Metall abgedeckt.

Prüfungsfrage

TC318  Um die Abstrahlungen der Spule eines abgestimmten Schwingkreises zu verringern, sollte die Spule ...
	in einem Abschirmbecher aus Metall untergebracht werden.
	in einem nichtmetallischen Harz eingehüllt werden.
	in einem Abschirmbecher aus Kunststoff untergebracht werden.
	einen abgestimmten Kunststoffkern aufweisen.

Reihen- und Parallelschaltung bei der Spule

Die Berechnung der Reihen- und Parallelschaltung bei Spulen erfolgt genau wie beim Widerstand. Bei der Reihenschaltung werden die Induktivitäten addiert und bei der Parallelschaltung erfolgt die Berechnung nach folgender Formel.

\[ \boxed{\frac{1}{L} = \frac{1}{L_1} + \frac{1}{L_2} + \frac{1}{L_3} + \cdots} \]

Prüfungsfrage

TD104  Wie groß ist die Gesamtinduktivität von drei in Reihe geschalteten Spulen von 2000 nH,  0,03 mH und 1500 µH?
	1532 µH
	1503 µH
	1873 nH
	1873 µH

Lösungsweg (hier klicken zum Anzeigen):

Prüfungsfrage

TD105  Wie groß ist die Gesamtinduktivität von drei parallel geschalteten Spulen von 2000 nH, 0,03 mH und 1500 µH?
	187,3 nH
	1,873 µH
	1532 µH
	1,532 µH

Lösungsweg (hier klicken zum Anzeigen):

R-L-C-Schaltungen

Wenn ein ohmscher Widerstand gleichzeitig mit einem Kondensator und einer Spule zusammengeschaltet ist, müssen die beiden entgegen gesetzten Phasenverschiebungen von Spule und Kondensator berücksichtigt werden. An einem Beispiel der Reihenschaltung soll dies einmal gezeigt werden. Es sei folgende Reihenschaltung (Bild 3-21) gegeben, X_L sei größer als X_C. Links wurden die einzelnen Widerstandspfeile gezeichnet. Um die Summe zu erhalten, werden alle Pfeile entsprechend ihrer Richtung aneinander gesetzt. Die Verbindung vom Anfang R bis zur Pfeilspitze X_C ist Z.

Prüfungsfrage

TD110  Was ist bei der Berechnung von Wechselstromkreisen, die Kombinationen von R, L und C enthalten, zu beachten?
	Spannungen, Ströme, Widerstände und Leistungen einzelner Komponenten müssen unter Beachtung der Thomsonschen Schwingungsgleichung addiert werden.
	Spannungen, Ströme, Widerstände und Leistungen einzelner Komponenten müssen unter Beachtung der Phasenwinkel geometrisch addiert werden.
	An Stelle des ohmschen Gesetzes tritt bei Blindwiderständen im Wechselstromkreis die Thomsonsche Schwingungsgleichung.
	Für jede Kombination von R, L und C gelten eigene ohmsche Gesetze.

Die Stromdichte

Besonders bei den geschlossenen Transformatoren (siehe weiter unten) darf in der Wicklung nicht zu viel Wärme entstehen. Weil aber jeder Kupferdraht einen (Verlust-)Widerstand hat, entsteht durch den Strom Verlustwärme. Deshalb wird für die Kupferdrähte häufig eine zulässige Stromdichte angegeben. Das ist der Strom pro Fläche des Drahtquerschnitts.

\[ S = \frac{I}{A} \quad \text{in} \quad \left[ \frac{\text{A}}{\text{mm}^2} \right] \]

Prüfungsfrage

TC403  Eine Transformatorwicklung hat einen Drahtdurchmesser von 0,5 mm. Die zulässige Stromdichte beträgt 2,5 A/mm². Wie groß ist der zulässige Strom?
	0,23 A
	0,49 A
	1,25 A
	1,96 A

Lösungsweg (hier klicken zum Anzeigen):

Übertrager – Transformator

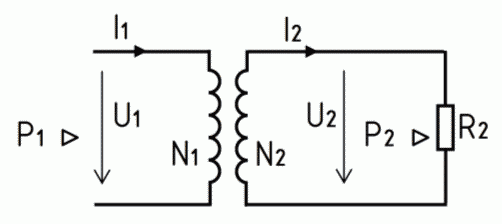
Werden zwei elektrisch getrennte Spulen von einem gemeinsamen Magnetfeld durchdrungen, zum Beispiel wenn sie auf einen gemeinsamen Kern gewickelt sind, kann die Wechselstromleistung P₁ auf die Sekundärseite als P₂ übertragen werden. Dabei verhalten sich die induzierten Spannungen in den Wicklungen wie deren Windungszahlen. Das Verhältnis der Windungszahlen N₁ zu N₂ nennt man Übersetzungsverhältnis ü.

\[ \text{ü} = \frac{N_1}{N_2} = \frac{U_1}{U_2} \]

Die Eingangswicklung eines Transformators nennt man Primärseite (mit N₁, U₁, I₁), die Ausgangswicklung Sekundärseite (mit N₂, U₂, I₂). Einen verlustlosen Transformator nennt man Übertrager.

Prüfungsfrage

TC401  Ein Trafo liegt an 230 Volt und gibt 11,5 Volt ab. Seine Primärwicklung hat 600 Windungen. Wie groß ist seine Sekundärwindungszahl?
	20 Windungen
	30 Windungen
	52 Windungen
	180 Windungen

Lösungsweg (hier klicken zum Anzeigen):

Es soll nachgewiesen werden, dass sich die Ströme umgekehrt verhalten wie die Spannungen. Nehmen wir einmal an, dass der Transformator keine Verluste hätte. Für einen verlustlosen Transformator gilt Eingangsleistung gleich Ausgangsleistung. \[ \begin{align} && P_1 &= P_2 \\ \text{oder} && \quad U_1 \cdot I_1 &= U_2 \cdot I_2 \\ \text{oder} && \quad \frac{U_1}{U_2} &= \frac{I_2}{I_1} \end{align} \] Also: Die Ströme verhalten sich umgekehrt wie die Spannungen.

Prüfungsfrage

TC402   Ein Transformator setzt die Spannung von 230 Volt auf 6 Volt herunter und liefert dabei einen Stom von 1,15 A. Wie groß ist der dadurch in der Primärwicklung zu erwartende Strom bei Vernachlässigung der Verluste?
	33,3 mA
	22,7 mA
	0,83 mA
	30 mA

Lösungsweg (hier klicken zum Anzeigen):

Übertrager

Bei geringen Leistungen spricht man bei einem Transformator von einem Übertrager. Es soll zunächst gezeigt werden, dass man mit einem Übertrager Widerstände "übersetzen" kann. Nehmen wir an, an den Ausgang des Übertragers wird ein Widerstand R₂ angeschlossen.

Bei einem verlustlosen Transformator (Übertrager) gilt

\[ \begin{align} P_1 & = P_2 &|& \ \text{setze } P = \frac{U^2}{R}\\ \frac{{U_1}^2}{R_1} & = \frac{{U_2}^2}{R_2} &|&\cdot \frac{R_1}{{U_2}^2}\\ \frac{{U_1}^2}{{U_2}^2} & = \frac{R_1}{R_2} &|&\ \text{Quadrat ausklammern}\\ \text{ü}^2 = \left(\frac{U_1}{U_2}\right)^2 & = \frac{R_1}{R_2} &|& \ R_2 \text{ oder } \sqrt{\cdots}\cdot \\ \boxed{ \text{ü}^2 \cdot R_2 = R_1} & \text{ oder } \boxed {\text{ü} = \sqrt{\frac{R_1}{R_2}} } \end{align} \]

Das übersetzungsverhältnis berechnet sich als Wurzel aus den Widerständen. Wenn man beispielsweise auf der Sekundärseite einen Widerstand von 400 Ohm anschließt und die Windungszahlen verhalten sich wie 1 zu 2 (primär zu sekundär), verhält sich der Übertrager so, dass man am Eingang einen Widerstand von einem Viertel feststellt, also 100 Ohm.

Prüfungsfrage

TC407  Für die Anpassung einer 50-Ω-übertragungsleitung an eine 600-Ω-Antenne wird ein Übertrager verwendet. Welches Windungszahlverhältnis sollte er aufweisen?
	1 : 1
	1: 3,5
	1 : 5,5
	1 : 12

Lösungsweg (hier klicken zum Anzeigen):

Prüfungsfrage

TC406  Für die Anpassung einer 300-Ω-Antenne an eine 75-Ω-übertragungsleitung kann ein Übertrager mit einem Windungszahlenverhältnis von
	4:1 verwendet werden.
	8:1 verwendet werden.
	2:1 verwendet werden.
	16:1 verwendet werden.

Prüfungsfrage

TC405  In dieser Schaltung ist R = 6,4 kΩ. Die Impedanz zwischen den Anschlüssen A und B beträgt
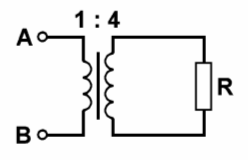	0,4 kΩ.
	25,6 kΩ.
	6,4 kΩ.
	1,6 kΩ.

Lösungsweg (hier klicken zum Anzeigen):

Prüfungsfrage

TC404  In dieser Schaltung ist R = 16 kΩ. Die Impedanz zwischen den Anschlüssen A und B beträgt
	64 kΩ
	16 kΩ
	4 kΩ
	1 kΩ

Der Balun-Transformator

In der Hochfrequenztechnik wird folgendes Transformatorprinzip gern eingesetzt. Der „Transformator“ besteht aus nur einer einzigen Wicklung mit Mittelanzapfung. Auch hier gilt: Die Spannungen verhalten sich wie die Windungszahlen und dies ist gleich dem Übersetzungsverhältnis.

  

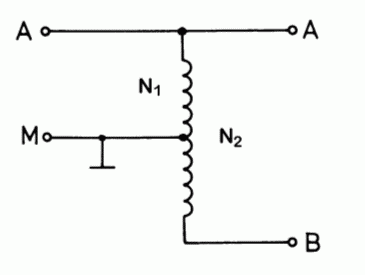
Anhand einer Formelumstellung will ich Ihnen zeigen, dass dieser Transformator bei Mittenanzapfung, das heißt wenn N₂ zweimal N₁ ist, Widerstände (Impedanzen) im Verhältnis 4 : 1 transformiert. Nehmen wir an, an der Wicklung N₂ (Klemmen A – B) ist ein Widerstand R₂ angeschlossen.

\[ \frac{N_1}{N_2} = \sqrt{\frac{R_1}{R_2}} \]

Diese Formel soll nach \( \frac{R_2}{R_1} \) umgestellt werden. Zunächst wird quadriert.

\[ \begin{align} \left(\frac{N_1}{N_2}\right)^2 = \frac{R_1}{R_2} \quad \text{oder} \quad \frac{R_2}{R_1} &= \left(\frac{N_2}{N_1}\right)^2\\ \text{Mit} \ N_2 = 2 \cdot N_1 \quad \text{wird} \quad \frac{R_2}{R_1} &= \left(\frac{2 \cdot N_1}{N_1}\right)^2 \\ N_1 \text{ kürzt sich heraus und } 2^2 &= 4 \\ \frac{R_2}{R_1} &= 4 \ \text{oder} \ \boxed{ R_2 = 4 \cdot R_1} \end{align} \]

Warum dieser Transformator „Balun“ (balanced - unbalanced) heißt, wird in der Lektion 10 unter „Symmetrierung“ erläutert.

Prüfungsfrage

TH419  Für welche Antennenimpedanz ist der obige Balun-Transformator aus zweimal 8 Windungen ausgelegt?
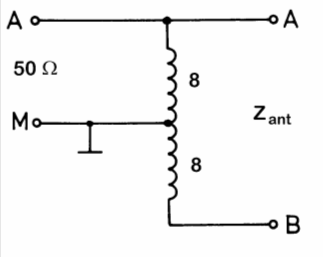	50 Ω
	100 Ω
	200 Ω
	400 Ω

Lösungsweg (hier klicken zum Anzeigen):

Prüfungsfrage

TH420  Obiger Balun-Transformator aus zweimal 8 Windungen ist gegeben. Von A nach B wird ein Faltdipol mit 200 Ohm Impedanz angeschlossen. Welche Impedanz misst man zwischen A und M?
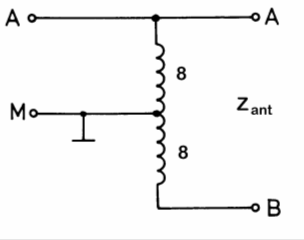	50 Ω
	100 Ω
	200 Ω
	400 Ω

Viel Erfolg beim Lehrgang wünscht Ihnen Eckart Moltrecht DJ4UF!

Nach Oben

Zur Lehrgangs-Übersicht Technik Klasse A

Copyright-Hinweis:
	Dieser DARC-Online-Lehrgang wurde mit freundlicher Genehmigung des Autors Eckart K. W. Moltrecht aus seinen Büchern "Amateurfunk-Lehrgang für das Amateurfunkzeugnis" aus dem VTH-Verlag (möglicherweise einer älteren Auflage!) für das Internet umgewandelt. Das Copyright liegt beim Autor und beim Verlag. Mehr über den Autor!
	Die Darstellung auch nur von Auszügen oder Zeichnungen oder Fotos im Internet ist untersagt. Für die private Verwendung können Sie gern eine Genehmigung beim Autor erhalten. Schreiben Sie eine E-Mail an eckart.moltrecht(at)gmail.com!

Letzte Bearbeitung: 16.06.2017 DJ4UF, 04.04.2020 DH8GHH
Fehlermeldungen mit Linkangabe an DH8GHH@darc.de