DARC-Online-Lehrgang Technik Klasse E Kapitel 3: Ohmsches Gesetz, Leistung, Arbeit
Neue Ausbildungsplattform 50ohm.de
Das Ausbildungsmaterial für den neuen Fragenkatalog (2024) findest du auf www.50Ohm.de
Hinweis: Der Lehrgang auf dieser Seite bezieht sich auf die alten Fragenkataloge, nach denen nur noch bis April 2024 geprüft wurde.
Kapitel 3: Ohmsches Gesetz, Leistung, Arbeit
In diesem Kapitel geht es um das wichtigste Gesetz der Elektrotechnik.
Inhaltsübersicht
Das Ohmsche Gesetz
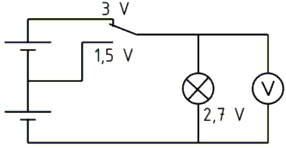
Ein einfacher Versuch nach Schaltung Bild 3-1 zeigt, dass es zwischen Spannung und Strom einen Zusammenhang gibt. Erhöht man beim Betrieb einer Glühlampe die Spannung, so leuchtet sie heller. Dies ist ein Zeichen, dass höherer Strom fließt.
Die Schaltung zeigt zwei in Reihe geschaltete Zellen von je 1,5 Volt. Mit dem Umschalter kann man auf die erste Zelle schalten und bekommt 1,5 Volt. Oder man schaltet auf die Reihenschaltung (Schalter oben) und die Betriebsspannung beträgt 3 Volt. Das Symbol mit dem Kreuz stellt eine Glühlampe als Verbraucher dar.
Dass nicht ein unendlich großer Strom fließt, liegt daran, dass der Leiterwerkstoff des Glühfadens in der Glühlampe dem Stromfluss einen Widerstand entgegensetzt. Dieser Widerstand wird sowohl von der vorhandenen Zahl der frei beweglichen Leitungselektronen als auch vom Atomgitteraufbau des Werkstoffes bestimmt.
Der Widerstand der Glühlampe oder jeder andere Widerstand kann allgemein durch folgendes Symbol dargestellt werden.
Die Größe eines Widerstandes wird mit dem Buchstaben R (resistor) gekennzeichnet, seine Einheit ist Ohm, abgekürzt Ω.
| Definition: Ein Widerstand hat den Wert R = 1 Ω (sprich: ein Ohm), wenn bei Anlegen einer Spannung von 1 Volt ein Strom von 1 Ampere fließt. |
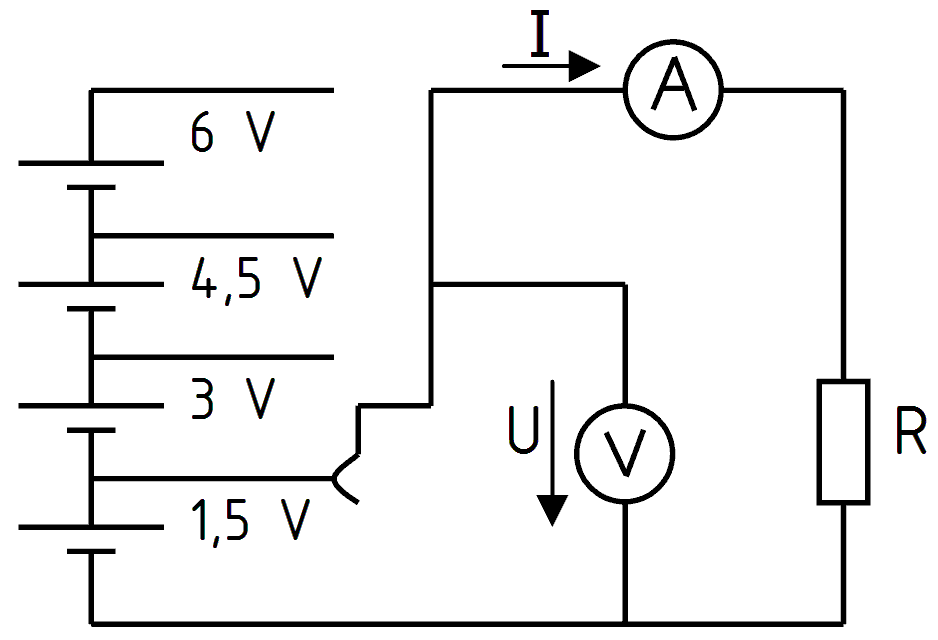
Mit einer verstellbaren Spannungsquelle, wie sie in Bild 3-2 dargestellt ist, soll der Zusammenhang zwischen Strom, Spannung und Widerstand genauer untersucht werden. Denken Sie sich vier Zellen von je 1,5 Volt in Serie geschaltet mit je einen Abgriff bei 1,5 V, 3 V, 4,5 V und 6 V. Es kann über einen Strommesser ein Lastwiderstand R angeschlossen werden.
Versuch 1
Bei einem festen Widerstand von R1 = 220 Ω wird die Spannung verändert und der Strom gemessen.
| Bei U = | 1,5 V | 3,0 V | 4,5 V | 6,0 V |
| beträgt I = | 6,8 mA | 13,6 mA | 20,5 mA | 27,3 mA |
Diese Messwerte sind im Diagramm Bild 3-3 bereits eingetragen. Nachgetragen ist noch der Messwert 0, denn ohne Spannung (U=0) fließt natürlich kein Strom (I=0).
| Versuch 2 Bei einem festen Widerstand von R1 = 100 Ω soll die Spannung verändert und der Strom gemessen werden. |
Wenn Sie keine Messmöglichkeit haben, verwenden Sie die in folgender Tabelle eingetragenen Werte.
| Bei U = | 1,5 V | 3,0 V | 4,5 V | 6,0 V |
| beträgt I = | 15 mA | 30 mA | 45 mA | 60 mA |
Tragen Sie diese Messwerte zusätzlich in das Diagramm Bild 3-3 ein! Es muss sich eine Gerade ergeben. Verlängern Sie die Gerade! Sie muss durch den Nullpunkt gehen, denn natürlich fließt kein Strom (I = 0 A), wenn keine Spannung (U = 0 A) anliegt.
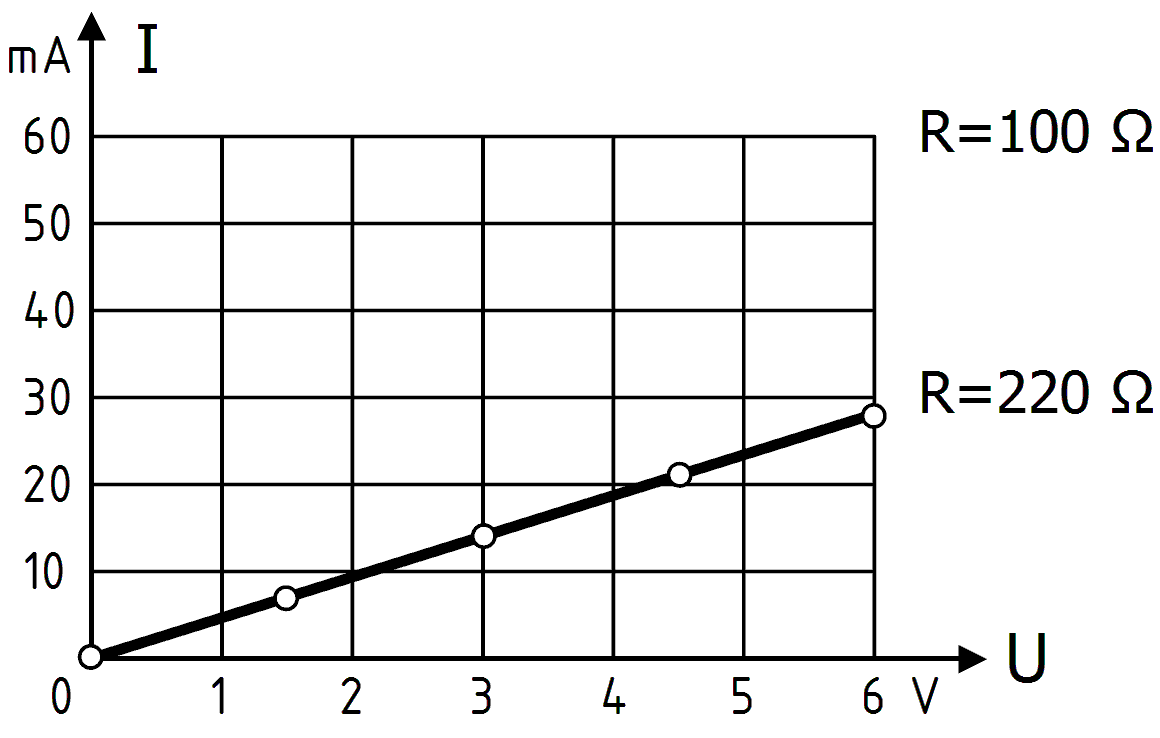
Aus dem Diagramm und aus der Tabelle kann man Folgendes erkennen: Bei Verdopplung der Spannung fließt genau der doppelte Strom, wenn man den Widerstand konstant lässt. Man sagt: Spannung und Strom sind proportional und schreibt
U ~ I (sprich: U proportional I).
Versuch 3
Es soll ein konstanter Strom von 20 mA fließen. Der Widerstand wird verändert und die notwendige Spannung gemessen.
| Bei R = | 75 Ω | 150 Ω | 300 Ω |
|---|---|---|---|
| benötigt man U = | 1,5 V | 3 V | 6 V |
Bei Verdopplung des Widerstandes benötigt man eine doppelt so große Spannung, damit der gleiche Strom fließt. Spannung und Widerstand sind also proportional.
U ~ R
Beide Zusammenhänge lassen sich als Formel schreiben und ergeben das Ohmsche Gesetz .
U = R · I
Der Widerstand R ist gewissermaßen der Proportionalitätsfaktor zwischen U und I . Die Grundform des Ohmschen Gesetzes lässt sich leicht merken, wenn man an den Schweizer Kanton URI denkt.
Testen Sie sich, indem Sie links auf die Fragezeichen klicken, aber nur einmal in jeder Tabelle!
ehemalige Prüfungsfrage
| TB903 Welche Spannung lässt einen Strom von 2 Ampere durch einen Widerstand von 50 Ohm fließen? | |
|---|---|
| 25 V | |
| 200 V | |
| 100 V | |
| 52 V | |
Sie haben die Frage gut beantwortet, wenn Sie in der linken Spalte nur einmal das Wort "Richtig" sehen und keinmal "Falsch".
Lösungsweg (hier klicken zum Anzeigen)
Durch Umstellen der Grundformel erhält man weitere Formen des Ohmschen Gesetzes .
\[ \begin{align} I = \frac{U}{R} && && R = \frac{U}{I} \end{align} \]Das Umstellen dieser Formel wurde in der Lektion 1 geübt. Kennen Sie das "URI-Dreieck"? Schauen Sie gegebenenfalls dort nach.
Das URI-Dreieck
Aus der letzten Formel ergibt sich die Einheitengleichung für Ohm.
ehemalige Prüfungsfrage
| TB902 Welcher der nachfolgenden Zusammenhänge ist richtig? | |
|---|---|
| U = R ⋅ I | |
| I = U ⋅ R | |
| R = I / U | |
| I = R / U | |
Mit Hilfe des Ohmschen Gesetzes sind die beiden Grundgrößen Strom und Spannung über den Widerstand miteinander verknüpft. Dieser Zusammenhang gilt für Gleichspannung und mit Einschränkungen auch für Wechselspannungen (Kapitel 2). Um eine Größe ausrechnen zu können, müssen die zwei anderen bekannt sein.
ehemalige Prüfungsfrage
| TB904 Welcher Widerstand ist erforderlich, um einen Strom von 3 Ampere bei einer Spannung von 90 Volt fließen zu lassen? | |
|---|---|
| 93 Ω | |
| 1/30 Ω | |
| 270 Ω | |
| 30 Ω | |
Lösungsweg (hier klicken zum Anzeigen):
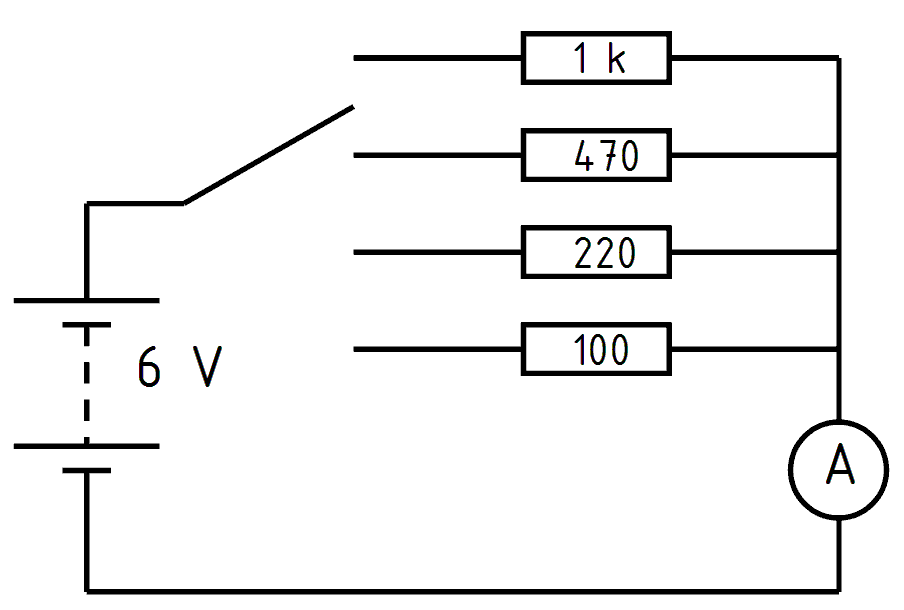
Versuch 4
Mit einem vierpoligen Taster nach Bild 3-4 werden nacheinander vier verschiedene Widerstände eingeschaltet. Welche Ströme werden jeweils gemessen?
Lösung: Tragen Sie die gemessenen Werte in folgende Tabelle ein. Wenn Sie keine Messmöglichkeit haben, können Sie natürlich auch rechnen.
| Bei R = | 100 Ω | 220 Ω | 470 Ω | 1 kΩ |
|---|---|---|---|---|
| misst man I = | ___ mA | ___ mA | ___ mA | ___ mA |
Prüfen Sie Ihre Ergebnisse folgendermaßen nach: Die Widerstände wurden jeweils etwa verdoppelt, dann muss der Strom jeweils ungefähr halb so groß werden.
Der Innenwiderstand
Wenn man einen Generator G, (Bild 3-5) zum Beispiel ein Netzteil, mit einem Verbraucher belastet, so dass viel Laststrom I fließt, geht die Spannung U an den Klemmen etwas zurück. Man sagt, ein Generator hat einen Innenwiderstand Ri, an dem eine Spannung abfällt.
Man berechnet den Innenwiderstand einer Spannungsquelle aus dem Spannungsunterschied Delta U (ΔU) an den Klemmen geteilt durch den Stromunterschied Delta I (ΔI) bei Belastung. Als Formel ausgedrückt schreibt man dafür
\[ R_i = \frac{\Delta U}{\Delta I} \]Diese Formel finden Sie in der BNetzA Formelsammlung (siehe auch Anhang 3 im Begleitbuch). Sie merken sich also einfach: Wie Ohmsches Gesetz , nur auf die Unterschiede (Delta) bei Belastung kommt es an.
ehemalige Prüfungsfrage
| TD302 Die Leerlaufspannung einer Gleichspannungsquelle beträgt 13,5 V. Wenn die Spannungsquelle einen Strom von 1 A abgibt, sinkt die Klemmenspannung auf 12,4 V. Wie groß ist der Innenwiderstand der Spannungsquelle? | |
|---|---|
| 1,1 Ω | |
| 1,2 Ω | |
| 12,4 Ω | |
| 13,5 Ω | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TD303 Die Leerlaufspannung einer Gleichspannungsquelle beträgt 13,5 V. Wenn die Spannungsquelle einen Strom von 2 A abgibt, sinkt die Klemmenspannung auf 13 V. Wie groß ist der Innenwiderstand der Spannungsquelle? | |
|---|---|
| 0,25 Ω | |
| 6,5 Ω | |
| 6,75 Ω | |
| 13 Ω | |
Und so kommt man an die Lösung:
Das können Sie doch allein, oder?
Übrigens: Eine „Spannungsquelle“ sollte einen niedrigen Innenwiderstand haben. Es gibt auch „Stromquellen“, die einen konstanten Strom liefern sollen. Diese müssen im Gegensatz zur Spannungsquelle einen großen Innenwiderstand haben. Mehr dazu im Lehrgang zur Klasse A.
ehemalige Prüfungsfrage
| TD301 Welche Eigenschaften sollten Strom- und Spannungsquellen aufweisen? | |
|---|---|
| Strom- und Spannungsquellen sollten einen möglichst niedrigen Innenwiderstand haben. | |
| Strom- und Spannungsquellen sollten einen möglichst hohen Innenwiderstand haben. | |
| Spannungsquellen sollten einen möglichst hohen Innenwiderstand und Stromquellen einen möglichst niedrigen Innenwiderstand haben. | |
| Spannungsquellen sollten einen möglichst niedrigen Innenwiderstand und Stromquellen einen möglichst hohen Innenwiderstand haben. | |
Die elektrische Leistung
Fließt durch einen Widerstand Strom, so wird in ihm eine Wärmeleistung erzeugt. Anwendungen sind Kochplatte, Bügeleisen, Heizspirale eines Elektroöfchens. Ein Widerstand in einer elektronischen Schaltung soll aber nicht heiß werden.
Die Leistung ist umso größer, je größer Strom und Spannung sind. Die elektrische Leistung P (englisch: power) ist das Produkt aus Spannung U und Strom I .
P = U · I
Die Maßeinheit für die elektrische Leistung ergibt sich aus dem Produkt Volt mal Ampere (V · A oder VA). Für die Leistung bei Gleichstrom wurde anstelle dieses Produktes die abgeleitete Einheit Watt (W) festgelegt.
1 W = 1 V · 1 A
ehemalige Prüfungsfrage
| TB901 Die Maßeinheit der elektrischen Leistung ist | |
|---|---|
| Joule. | |
| Kilowattstunden. | |
| Amperestunden. | |
| Watt. | |
Neben dieser Einheit gibt es auch wieder Vielfache oder Teile der Einheit.
| 1 Megawatt | 1 MW | 106 W | 1 000 000 W |
| 1 Kilowatt | 1 kW | 103 W | 1 000 W |
| 1 Milliwatt | 1 mW | 10-3 W | 1/1000 W |
| 1 Mikrowatt | 1 µW | 10-6 W | 1/1000000 W |
Die Formel P = U ⋅ I gilt grundsätzlich bei Gleichstrom. Bei Wechselstrom gilt sie nur dann, wenn keine Phasenverschiebung zwischen Strom und Spannung auftritt, wenn nur eine so genannte rein Ohmsche Belastung vorliegt. In den folgenden Aufgaben mit Wechselstrom oder Hochfrequenz wird angenommen, dass eine solche Ohmsche Belastung vorliegt. Näher soll hier im Rahmen des Amateurfunklehrgangs Klasse E nicht darauf eingegangen werden. In der theoretischen Elektrotechnik heißt dieses Kapitel Wechselstromtechnik und beinhaltet höhere Mathematik.
ehemalige Prüfungsfrage
| TB908 Ein mit einer künstlichen 50-Ω-Antenne in Serie geschaltetes HF-Amperemeter zeigt 2 A an. Welche Leistung gibt der Sender ab? | |
|---|---|
| 100 W | |
| 200 W | |
| 25 W | |
| 250 W | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB907 Der Effektivwert der Spannung an einer künstlichen 50-Ω-Antenne wird mit 100 V gemessen. Die Leistung an der Last beträgt | |
|---|---|
| 141 W | |
| 100 W | |
| 283 W | |
| 200 W | |
ehemalige Prüfungsfrage
| TB911 Welche Belastbarkeit muss ein Vorwiderstand haben, an dem bei einem Strom von 50 mA eine Spannung von 50 V abfallen soll? | |
|---|---|
| 25 W | |
| 250 mW | |
| 2,5 W | |
| 1 W | |
ehemalige Prüfungsfrage
| TB910 Ein 100-Ω-Widerstand, an dem 10 V anliegen, muss mindestens eine Belastbarkeit haben von | |
|---|---|
| 0,01 W. | |
| 100 mW. | |
| 1 W. | |
| 10 W. | |
ehemalige Prüfungsfrage
| TB909 Ein Mobiltransceiver (Sender?Empfänger) hat bei Sendebetrieb eine Leistungsaufnahme von 100 Watt aus dem 12-V-Bordnetz des Kraftfahrzeuges. Wie groß ist die Stromaufnahme? | |
|---|---|
| 1200 A | |
| 16,6 A | |
| 8,33 A | |
| 0,12 A | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB906 Eine Glühlampe hat einen Nennwert von 12 V und 48 W. Bei einer 12-V-Versorgung beträgt die Stromentnahme | |
|---|---|
| 36 A. | |
| 250 mA. | |
| 750 mA. | |
| 4 A. | |
Die Rechnung erfolgt wie bei der Aufgabe zuvor.
Die elektrische Arbeit
Wie auch in der Mechanik ist die elektrische Arbeit W (englisch: work) umso größer, je länger eine Leistung verrichtet wird.
Arbeit = Leistung · Zeit
W = P · t
Dieses Gesetz gilt auch in der Elektrotechnik. Setzt man für die Leistung noch Strom mal Spannung ein, kann man für die elektrische Arbeit auch schreiben
W = U · I · t
Die Maßeinheit ergibt sich aus dieser Formel, indem man die Grundeinheiten Volt, Ampere und Sekunde einsetzt, also VAs oder Ws (Volt · Ampere = Watt), also Wattsekunden.
Merken Sie sich: Die Einheit der Arbeit ist 1 Wattsekunde (1 Ws)
Für größere Arbeit ist diese Einheit etwas unpraktisch. Im Haushalt verwendet man besser Kilowattstunden.
ehemalige Prüfungsfrage
| Übungsaufgabe üB301 Wie viel Wattsekunden hat eine Kilowattstunde? | |
|---|---|
| 3 600 Ws | |
| 60 000 Ws | |
| 3 600 000 Ws | |
| 60 Ws | |
Lösungsweg (hier klicken zum Anzeigen):
| Übungsaufgabe ÜB302 Ein Computer nimmt 120 Watt Leistung auf. a) Wie groß ist der "Stromverbrauch" (elektrische Arbeit oder Energie* in Kilowattstunden), wenn dieser den ganzen Tag von 8 bis 18 Uhr eingeschaltet bleibt? b) Wie hoch sind die "Stromkosten" (Kosten für die erbrachte elektrische Arbeit), wenn für eine Kilowattstunde 25 Cent bezahlt werden muss? |
Lösung
a) W = P · t = 120 W · 10 h = 1200 Wh = 1,2 kWh
b) Kosten K = 1,2 kWh ? 25 Cent/kWh = 30 Cent
Es müssen 30 Cent dafür bezahlt werden. Betreibt man den Computer täglich zehn Stunden, kommen 30 mal 30 Cent gleich 9,00 Euro an Stromkosten für einen Monat zusammen.
ehemalige Prüfungsfrage
| TB905 Eine Stromversorgung nimmt bei 230 Volt einen Strom von 0,63 Ampere auf. Welche elektrische Arbeit wird bei einer Betriebsdauer von 7 Stunden verbraucht? | |
|---|---|
| 1,01 kWh | |
| 0,1 kWh | |
| 2,56 kWh | |
| 20,7 kWh | |
Und so kommt man an die Lösung:
W = P · t = U · I · t
W = 230 V · 0,63 A · 7 h = 1014 Wh
W= 1,01 kWh
*Energie
Gespeicherte Arbeit wird in der Elektrotechnik auch elektrische Energie genannt. Ein Akku kann beispielsweise 60 Wattstunden an Energie abgeben. Oder die Energiekosten für den Computer in obigem Beispiel betragen 9,00 Euro im Monat.
Viel Erfolg beim Lehrgang wünscht Ihnen Eckart Moltrecht DJ4UF!
| Copyright-Hinweis: | |
|---|---|
 | Dieser DARC-Online-Lehrgang wurde mit freundlicher Genehmigung des Autors Eckart K. W. Moltrecht aus seinen Büchern "Amateurfunk-Lehrgang für das Amateurfunkzeugnis" aus dem VTH-Verlag (möglicherweise einer älteren Auflage!) für das Internet umgewandelt. Das Copyright liegt beim Autor und beim Verlag. Mehr über den Autor! |
 | Die Darstellung auch nur von Auszügen oder Zeichnungen oder Fotos im Internet ist untersagt. Für die private Verwendung können Sie gern eine Genehmigung beim Autor erhalten. Schreiben Sie eine E-Mail an eckart.moltrecht(at)gmail.com! |
Letzte Bearbeitung: 24.05.2017 DJ4UF, 04.04.2020 DH8GHH
Fehlermeldungen mit Linkangabe an DH8GHH@darc.de
