DARC-Online-Lehrgang Technik Klasse E Kapitel 4: Der Widerstand und seine Grundschaltungen
Neue Ausbildungsplattform 50ohm.de
Das Ausbildungsmaterial für den neuen Fragenkatalog (2024) findest du auf www.50Ohm.de
Hinweis: Der Lehrgang auf dieser Seite bezieht sich auf die alten Fragenkataloge, nach denen nur noch bis April 2024 geprüft wurde.
Kapitel 4: Der Widerstand und seine Grundschaltungen
In diesem Kapitel geht es um spezielle Begriffe zum Widerstand und um Widerstandsschaltungen.
Inhaltsübersicht
- Spezifischer Widerstand
- Bauformen der Widerstände
- Kennzeichnung bei SMD
- Die Leitfähigkeit
- Farbcode
- Toleranzschema
- Reihenschaltung
- Parallelschaltung
Der Widerstand
Sie haben im Kapitel E02 gelernt, dass elektrischer Strom dann fließt, wenn elektrische Ladungsträger bewegt werden. Bei Nichtleitern (Isolatoren) kann keine Ladung bewegt werden, weil die Elektronen fest an die Atomkerne gebunden sind.
Bei Metallen sind die Elektronen schon bei normaler Zimmertemperatur im gesamten Atomverband frei beweglich. Damit stehen bei Metallen genügend freie Ladungsträger zum Transport von elektrischen Ladungen zur Verfügung. Deshalb leiten Metalle gut.
Ein Kubikzentimeter Kupfer besitzt zum Beispiel 1023(das ist eine 1 mit 23 Nullen) frei bewegliche Elektronen. Deshalb kann bei angelegter Spannung ein starker Strom fließen.
Fließt ein Strom durch einen Leiter, zum Beispiel durch den Glühfaden einer Glühlampe, müssen sich die Elektronen zwischen den Atomen des Leiters "hindurchzwängen". Die Atome sind außerdem schon bei Zimmertemperatur nicht in Ruhe, sondern vibrieren hin und her und zwar umso stärker, je höher die Temperatur ist.
Die beweglichen Ladungsträger haben auf ihrem Weg durch den Leiter ständig Zusammenstöße mit den Atomen und werden dadurch abgebremst. Der Leiter setzt somit dem Stromfluss einen Widerstand entgegen. Dieser Widerstand wird elektrischer Widerstand genannt.
Spezifischer Widerstand
Wovon hängt es ab, wie groß ein Widerstand tatsächlich ist? Bei langen Drähten müssen auf dem Weg viele "Hindernisatome" überwunden werden. Damit steigt auch der Widerstand mit zunehmender Länge. Je geringer die Querschnittsfläche ist, desto stärker werden die Ladungsträger behindert.
Der Widerstand R ist also umso größer je größer die Länge l des Leiters und je kleiner die Querschnittsfläche A ist.
Außerdem hängt der Widerstand noch vom Material des Leiters ab, denn es gibt gute und schlechte Leiter, je nachdem wie viele freie Elektronen vorhanden sind. Diese Materialkonstante wird spezifischer Widerstand ρ (griechisch: rho) genannt.
Je kleiner der Wert des spezifischen Widerstandes ist, desto besser leitet der Leiter. Silber (folgende Tabelle) hat eine bessere Leitfähigkeit als Gold. Gold oxidiert nur nicht und ist deshalb besser für Kontakte geeignet als Silber. Zinn (Lötzinn) leitet also relativ schlecht im Vergleich zu Kupfer. Kupferdrähte sollte man also am Ende nicht verzinnen, wenn sie als Kontakte dienen sollen.
| Werkstoff | Spezifischer Widerstand | Leitfähigkeit |
|---|---|---|
| Silber | 0,016 | 63 |
| Kupfer | 0,0178 | 56 |
| Gold | 0,022 | 45 |
| Aluminium | 0,027 | 37 |
| Eisen | 0,100 | 10 |
| Zinn | 0,115 | 8 |
| Blei | 0,208 | 5 |
| Quecksilber | 0,958 | 1 |
| \( \frac{Ω \cdot \text{mm}^2}{\text{m}} \) | \( \frac{\text{m}}{Ω \cdot \text{mm}^2} \) |
Tabelle 4-1: Spez. Widerstand und Leitfähigkeit
Die Leitfähigkeit
Häufig wird anstatt des spezifischen Widerstandes die spezifische Leitfähigkeit κ (griechischer Buchstabe kappa) des Werkstoffes angegeben. Die Leitfähigkeit ist jedoch nichts anderes als der Kehrwert des spezifischen Widerstandes. Mit dem Kehrwert erhält man Zahlen größer als 1, die sich leichter merken lassen als diese 0,0...-Werte.
Beispiel
Wie groß ist die elektrische Leitfähigkeit von Kupfer?
Lösung: Den spezifischen Widerstand entnehmen wir der Tabelle und berechnen den Kehrwert.
\[ \kappa = \frac{1}{\rho} = \frac{1 \ \text{m}}{0,0178 \ Ω \cdot \text{mm}^2} = 56 \cdot \frac{\text{m}}{Ω \cdot \text{mm}^2} \]Der Wert 56 ist "handlicher" als 0,0178. Je größer die Zahl ist, desto besser ist die Leitfähigkeit (Tabelle 4-1 rechte Spalte).
ehemalige Prüfungsfrage
| TB101 Welche Gruppe enthält insgesamt die besten gut leitenden Metalle? | |
|---|---|
| Silber, Kupfer, Blei | |
| Silber, Kupfer, Aluminium | |
| Kupfer, Eisen, Zinn | |
| Aluminium, Kupfer, Quecksilber | |
ehemalige Prüfungsfrage
| TB102 Welches der genannten Metalle hat die beste elektrische Leitfähigkeit? | |
|---|---|
| Kupfer | |
| Gold | |
| Silber | |
| Zinn | |
ehemalige Prüfungsfrage
| TB103 Welches der genannten Metalle hat die schlechteste elektrische Leitfähigkeit? | |
|---|---|
| Kupfer | |
| Gold | |
| Aluminium | |
| Zinn | |
Nichtleiter, Halbleiter
Nichtleiter (Isolatoren) sind solche Werkstoffe, die den Strom praktisch gar nicht leiten. Man benötigt sie, um zwei Leiter voneinander zu isolieren. Zu den Nichtleitern gehören die meisten Kunststoffe sowie Glas, Porzellan, trockenes Holz. Halbleiter sind nicht einfach schlechte Leiter, sondern sie leiten Strom nur unter bestimmten Bedingungen (siehe Lektion 13).
ehemalige Prüfungsfrage
| TB104 Welche Gruppe von Materialien enthält nur Nichtleiter? | |
|---|---|
| Pertinax, Polyvinylchlorid (PVC), Graphit | |
| Epoxid, Polyethylen (PE), Polystyrol (PS) | |
| Polyethylen (PE), Messing, Konstantan | |
| Teflon, Pertinax, Bronze | |
Bauformen der Widerstände
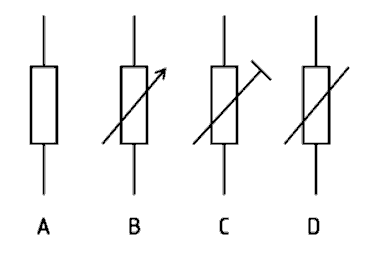
Widerstände werden in Festwiderstände, einstellbare und veränderliche Widerstände eingeteilt. Bei einstellbaren Widerständen ist der Widerstandswert durch den Anwender (meist mechanisch) veränderbar (Potentiometer und Trimmer, Bild 4-2 oder 4-3). Bei veränderlichen Widerständen ändert sich der Widerstand durch den Einfluss einer physikalischen Größe, beispielsweise durch Temperatur oder durch Spannung (Bild 4-4).
Im Bild 4-1 ist links (A) das Schaltzeichen eines Widerstandes allgemein dargestellt. Bild B zeigt einen von außen bedienbaren einstellbaren Widerstand, zum Beispiel ein Lautstärkeeinsteller. Man nennt ihn auch Potentiometer (Bild 4-2). Bild 4-1C zeigt ebenfalls einen einstellbaren Widerstand, allerdings ist er nicht von außen bedienbar, sondern wird intern im Gerät durch ein Werkzeug (Schraubendreher) verstellt, um einmalig Werte einzustellen.
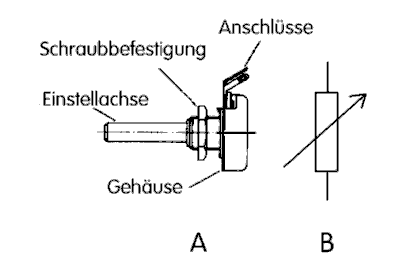
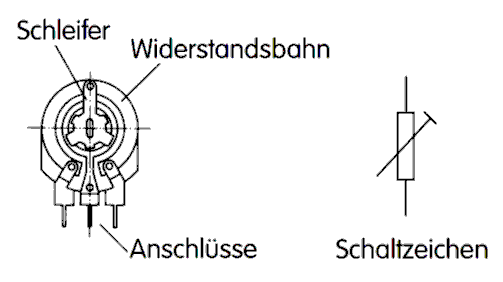
Solch ein Potentiometer (Bild 4-3) nennt man Trimmer. Bild 4-1 D dient als allgemeines Schaltzeichen für einen einstellbaren Widerstand. Es kann ein Potentiometer oder ein Trimmer sein.
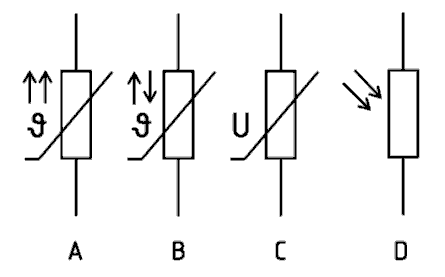
In den Bildern 4-4A und B sind Widerstände dargestellt, die ihren Wert in Abhängigkeit von der Temperatur ändern. Die gleichläufigen Pfeile bedeuten: Je höher die Temperatur, desto höher der Widerstand. Man nennt solch einen Widerstand einen PTC, weil er einen positiven Temperaturkoeffizienten hat. Der Widerstand Bild B ist ein NTC (negativer Temperaturkoeffizient). Bei ihm verringert sich der Widerstand, wenn die Temperatur steigt. Bild C ist ein spannungsabhängiger Widerstand (voltage dependend resistor VDR). Bild D zeigt einen lichtabhängigen Widerstand (light dependend resistor, LDR). Die beiden von links oben kommenden Pfeile in Bild 4-4D sollen den Lichteinfall beim LDR andeuten.
ehemalige Prüfungsfrage
| TC106 Welches der folgenden Bauteile ist ein NTC? | |
|---|---|
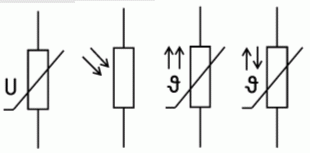 A B C D | |
| Bauteil A | |
| Bauteil B | |
| Bauteil C | |
| Bauteil D | |
ehemalige Prüfungsfrage
| TC105 Welches Bauteil hat folgendes Schaltzeichen? | |
|---|---|
| | |
| LDR | |
| VDR | |
| NTC | |
| PTC | |
ehemalige Prüfungsfrage
| TC107 Welches der folgenden Bauteile ist ein PTC? | |
|---|---|
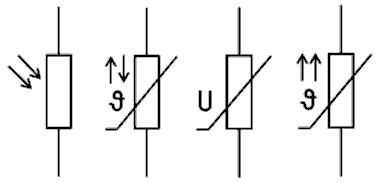 A B C D | |
| Bauteil A | |
| Bauteil B | |
| Bauteil C | |
| Bauteil D | |
Festwiderstände
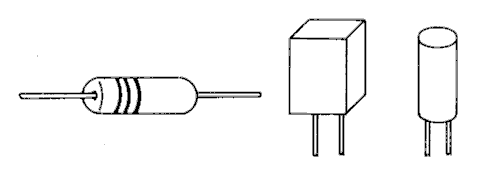
Bei Festwiderständen unterscheidet man Kohleschichtwiderstände, Metalloxidwiderstände, Metallschichtwiderstände und Drahtwiderstände. Kohleschichtwiderstände haben als Widerstandswerkstoff eine dünne Kohleschicht, die auf einen Träger aufgedampft wird. Große Widerstandswerte erreicht man durch Einschleifen einer durchgehenden Wendel über die gesamte Länge des Widerstandes. Die Kohleschicht wird durch einen eingebrannten Lack- oder Kunstharzüberzug geschützt und der Widerstandswert mit Farbringen gekennzeichnet. Diese Widerstandswerte gibt es für Leistungen (Belastbarkeit) zwischen 1/10 und 2 Watt. Die Größe der Widerstände ist ein Maß für ihre Belastbarkeit (Bild 4-7).
Metalloxidwiderstände sind induktionsarm, eignen sich deshalb für sehr hohe Frequenzen und haben eine wesentlich größere Belastbarkeit als Kohleschichtwiderstände gleicher Abmessungen.
ehemalige Prüfungsfrage
| TC109 Welche Bauart von Widerstand folgender Auswahl ist am besten für eine künstliche Antenne (Dummy Load) geeignet? | |
|---|---|
| Ein Metalloxidwiderstand | |
| Ein Kohleschichtwiderstand | |
| Ein keramischer Drahtwiderstand | |
| Ein frei gewickelter Drahtwiderstand aus Kupferdraht | |

Metallschichtwiderstände haben eine Edelmetallschicht (EMS) als Widerstandsmaterial oder ein dünner Metallfilm bildet die Widerstandsschicht. Diese Widerstände haben enge Toleranzen und werden als Präzisionswiderstände in der Messtechnik verwendet.
Drahtwiderstände (Bild 4-6) bestehen aus einem Wickel aus Widerstandsdraht auf einem keramischen Isolierkörper. Sie haben höhere Belastbarkeiten als Schichtwiderstände aber den Nachteil der Frequenzabhängigkeit wegen der großen Induktivitäten durch die Wicklung. Drahtwiderstände gibt es glasiert und zementiert.

Internationaler Farbcode
Früher hat man den Nennwert des Widerstandes als Zahlenwert aufgedruckt. Allerdings musste man beim Einbau auf die Lage der Widerstände achten, damit die Beschriftung von oben sichtbar bleibt. Bei der automatischen Bestückung bei Leiterplatten ist dies schwierig zu erreichen.
Beim internationalen Farbcode werden die Nennwerte in Form von Farbringen nach einem festgelegten Code aufgedruckt. Man zählt die Ringe von außen nach innen. Bei Widerständen mit axialen Anschlüssen sind die Ringe so verteilt, dass sie einem Ende näher sind. Dies ist der erste Ring und damit die erste Ziffer der Kennzeichnung. Der nächste Ring ist die zweite Ziffer und als dritter oder vierter Ring folgt der Multiplikator. Siehe Formelsammlung!
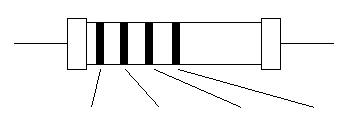
| Farbring | 1.Ziffer | 2.(3.)Ziffer | Nullen (Multiplikator) | Toleranz |
|---|---|---|---|---|
| schwarz | - | 0 | - | - |
| braun | 1 | 1 | 0 | ± 1% |
| rot | 2 | 2 | 00 | ± 2% |
| orange | 3 | 3 | 000 | - |
| gelb | 4 | 4 | 0000 | - |
| grün | 5 | 5 | 00000 | ±0,5% |
| blau | 6 | 6 | 000000 | - |
| violett | 7 | 7 | - | - |
| grau | 8 | 8 | - | - |
| weiß | 9 | 9 | - | - |
| gold | - | - | · 0,1 | ± 5% |
| silbern | - | - | · 0,01 | ± 10% |
| ohne | - | - | - | ± 20% |
Tabelle 4-2: Internationaler Farbcode
Es gibt Widerstände mit 4 und mit 5 Ringen. Beim System mit 4 Ringen bedeuten die ersten drei Ringe den Wert (Ziffer und Multiplikator) und der vierte Ring die Toleranz. Beim System mit fünf Ringen für Präzisionswiderstände benötigt man 4 Ringe für den Wert und der 5. Ring bedeutet die Toleranz.
Die ersten Ringe bedeuten jeweils eine Ziffer, der Ring vor der Toleranz bedeutet die Zehnerpotenz als Multiplikator oder Anzahl der Nullen (Tabelle 4-2). Die Farbe rot (2) beim Multiplikator beispielsweise bedeutet mal 10^2 oder mal 100, also zwei Nullen anhängen.
ehemalige Prüfungsfrage
| TC101 Die Farbringe gelb, violett und orange auf einem Widerstand mit 4 Farbringen bedeuten einen Widerstandswert von | |
|---|---|
| 4,7 kΩ | |
| 47 kΩ | |
| 470 kΩ | |
| 4,7 MΩ | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TC104 Die Farbringe rot, violett und rot auf einem Widerstand mit 4 Farbringen bedeuten einen Widerstand von | |
|---|---|
| 2,7 MΩ | |
| 27 kΩ | |
| 270 kΩ | |
| 2,7 kΩ | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TC102 Die Farbringe gelb, violett und rot auf einem Widerstand mit 4 Farbringen bedeuten einen Widerstandswert von | |
|---|---|
| 4,7 kΩ | |
| 47 kΩ | |
| 470 kΩ | |
| 4,7 MΩ | |
ehemalige Prüfungsfrage
| TC103 Die Farbringe rot, violett und orange auf einem Widerstand mit 4 Farbringen bedeuten einen Widerstandswert von | |
|---|---|
| 27 kΩ | |
| 2,7 kΩ | |
| 270 kΩ | |
| 2,7 MΩ | |
Zu den Multiplikatoren gold oder silbern gibt keine Prüfungsfrage in der Prüfung für die Klasse E. Den Farbcode brauchen Sie nicht auswendig zu lernen. Er steht in der Prüfungs-Formelsammlung der BNetzA.
Kennzeichnung bei SMD
Bei der SMD-Technik (surface mounted device) haben die Bauteile sehr geringe Abmessungen im Millimeterbereich. Die flache Oberfläche gestattet einen Aufdruck von drei bis vier kleinen Ziffern. Dabei gilt folgendes Kennzeichnungs-System.
Bei Werten bis 976 Ω stellt R den Dezimalpunkt dar.
3-stelliger Code: Zählweise wie beim Farbcode
4-stelliger Code: Zählweise wie beim Farbcode
ehemalige Prüfungsfrage
| TC110 Welchen Wert hat ein SMD-Widerstand mit der Kennzeichnung 221? | |
|---|---|
| 221 Ω | |
| 220 Ω | |
| 22 Ω | |
| 22 kΩ | |
ehemalige Prüfungsfrage
| TC111 Welchen Wert hat ein SMD-Widerstand mit der Kennzeichnung 223? | |
|---|---|
| 22 Ω | |
| 221 Ω | |
| 22 kΩ | |
| 220 Ω | |
Das Toleranzschema
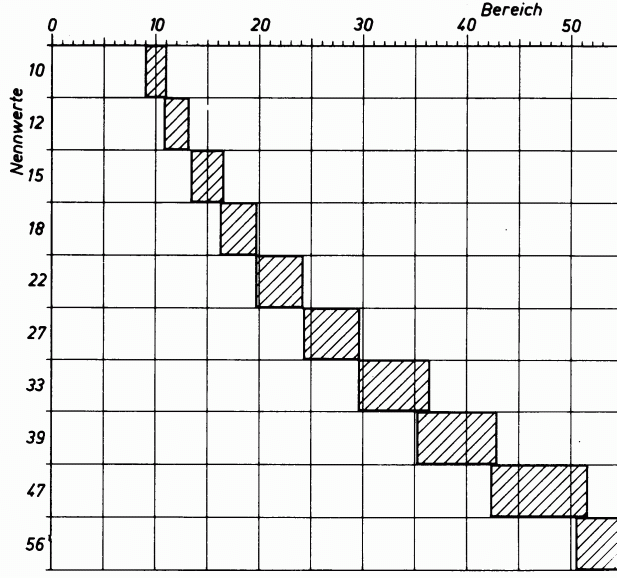
Sie werden sicher schon selbst festgestellt haben, dass es nicht alle Werte von Widerständen gibt. In der IEC-Reihe E12 mit 10% Toleranz (silberne Reihe) gibt es folgende bevorzugte Widerstandswerte pro Dekade. Eine Dekade geht immer von 1,1 bis 9,9 oder von 10 bis 99 oder 100 bis 990 usw.
10 – 12 – 15 – 18 – 22 – 27 – 33 – 39 – 47 – 56 – 68 – 82
Die internationale Normreihe E12 geht in dieser Form von 1 Ohm bis 10 Megohm. Also gibt es auch die Werte: 100 – 120 – 150 und so weiter oder 1,0 – 1,2 – 1,5 usw.
Diese Normreihe E12 mit den zwölf Widerstandswerten pro Dekade entsteht durch die Auslieferungstoleranz von ± 10 %. Die Überschneidung
erkennt man im Diagramm Bild 4-8.
Beispiel: Welchen größten und welchen kleinsten Wert können ein Widerstand von 18 kΩ und der nächste mit 22 kΩ jeweils in der Normreihe E12 haben?
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TC108 Ein Widerstand hat eine Toleranz von 10 %. Bei einem nominalen Widerstandswert von 5,6 kΩ liegt der tatsächliche Wert zwischen … | |
|---|---|
| 4760 und 6440 Ω. | |
| 5040 und 6160 Ω. | |
| 4,7 und 6,8 kΩ. | |
| 5,2 und 6,3 kΩ. | |
Reihen- und Parallelschaltung von Widerständen
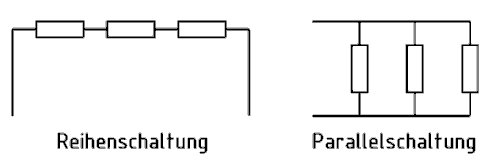
Die Zusammenschaltung von Widerständen lässt sich auf zwei Grundformen zurückführen: Reihenschaltung und Parallelschaltung (Bild 4-9). Die Reihenschaltung wird auch Serienschaltung genannt.
Eine Reihenschaltung entsteht, wenn man das Ende des ersten Widerstandes mit dem Anfang des zweiten verbindet und so weiter (Bild 4-9 links).
Bei der Parallelschaltung sind alle Anfänge und alle Enden jeweils miteinander verbunden und liegen damit alle direkt an der Spannungsquelle (Bild 4-9 rechts).
Die Reihenschaltung
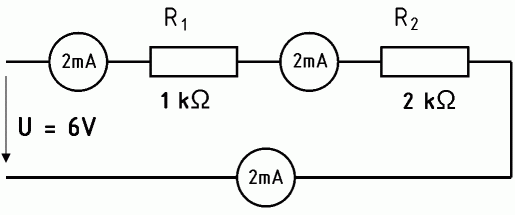
Zunächst wollen wir die Gesetzmäßigkeiten für die Reihenschaltung herleiten. Messen Sie einmal den Strom einer Reihenschaltung nach Bild 4-11 an verschiedenen Stellen. Er zeigt überall den gleichen Wert. Aus keinem Widerstand fließt mehr Strom heraus als hinein fließt.
Merke: In einer Reihenschaltung ist der Strom überall gleich groß.
Berechnen wir in obigem Beispiel (Schaltung Bild 4-11) die Spannungen an den beiden Widerständen.
U1 = R1 · I = 1 kΩ×2 mA = 2 V
U2 = R2 × I = 2 kΩ×2 mA = 4 V
Zusammen müssen sich die 6 V ergeben.
Merke: In einer Reihenschaltung sind die Teilspannungen zusammen so groß wie die Gesamtspannung.
U = U1 + U2 = 2 V + 4 V = 6 V
Die Gesamtspannung liegt dabei an dem Gesamtwiderstand der zwei Widerstände:
U = R · I = 6 V
Setzt man die Werte aus Bild 4-11 ein mit
U = R × I, U1 = R1 × I und U2 = R2 × I,
erhält man
R × I = R1 × I + R2 × I = I · (R1 + R2)
Da der Strom überall gleich ist, kann der Buchstabe I auf beiden Seiten der Gleichung gekürzt werden. Man erhält damit die Formel für die Reihenschaltung.
Merke: In einer Reihenschaltung sind die Teilwiderstände zusammen so groß wie die Gesamtwiderstand.
Dies gilt auch für mehr als zwei Widerstände, zum Beispiel
R = R1 + R2 + R3
Noch eine vierte „Gesetzmäßigkeit“ kann an diesem Beispiel abgeleitet werden. Betrachten Sie noch einmal die Ergebnisse der Spannungsberechnung aus der Schaltung Bild 4-11: Am 1-kΩ-Widerstand beträgt die Spannung 2 Volt und am doppelt so großen 2-kΩ-Widerstand beträgt sie 4 Volt.
Merken Sie sich: Bei der Reihenschaltung verhalten sich die Teilspannungen wie die zugehörigen Widerstände.
Diese Aussage lässt sich auch als Formel schreiben und führt uns dann zum nächsten Abschnitt.
\[ \frac{U_1}{U_2} = \frac{R_1}{R_2} \]Eine wichtige Anwendung der Reihenschaltung von Widerständen ist nämlich, aus einer höheren Spannung eine Teilspannung zur Spannungsversorgung einer elektronischen Schaltung zu gewinnen.
Der Spannungsteiler
Der letzte Merksatz lässt sich auch folgendermaßen ausdrücken:
In einer Reihenschaltung verhält sich die Teilspannung zur Gesamtspannung wie der Teilwiderstand zum Gesamtwiderstand (siehe Bild 4-12).
Als Formel geschrieben:
\[ \frac{U_1}{U} = \frac{R_1}{R} \ \text{oder} \ \frac{U_2}{U} = \frac{R_2}{R} \]Hier im Beispiel gilt:
\[ \frac{2 \ \text{V}}{6 \ \text{V}} = \frac{1 \ \text{kΩ}}{3 \ \text{kΩ}} \ \text{oder} \ \frac{4 \ \text{V}}{6 \ \text{V}} = \frac{2 \ \text{kΩ}}{3 \ \text{kΩ}} \]
Merke: Großer Spannungsabfall am großen Teilwiderstand, kleiner Spannungsabfall am kleinen Teilwiderstand.
Dies führt uns zu folgender Prüfungsaufgabe zum Spannungsteiler.
ehemalige Prüfungsfrage
| TD108 Die Gesamtspannung U an folgendem Spannungsteiler beträgt 12,2 V. Die Widerstände haben die Werte R1 = 10 kΩ und R2 = 2,2 kΩ. Wie groß ist die Teilspannung U2 ? | |
|---|---|
| 2,20 V | |
| 2,64 V | |
| 10.0 V | |
| 1,22 V | |
Lösungsweg (hier klicken zum Anzeigen):
Die Parallelschaltung von Widerständen

Eine Parallelschaltung entsteht, wenn man alle Anfänge und alle Enden der Bauteile miteinander verbindet (Bild 4-13).
Praxis
Schließen Sie je einen Widerstand von 1 kΩ, 2,2 kΩ und 4,7 kΩ in Parallelschaltung an eine Spannungsquelle mit U = 6 V und messen Sie alle Teilströme und den Gesamtstrom.
Sie müssten die in Bild 4-14 gezeigten Messergebnisse erzielen.
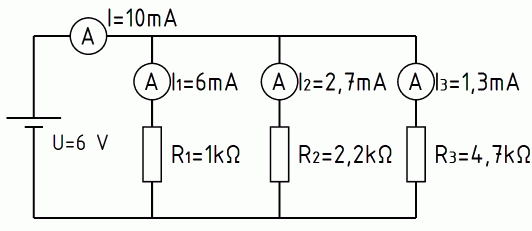
Messen Sie auch die Spannungen an jedem der Widerstände! Aus diesen Versuchsergebnissen lassen sich folgende wichtige Gesetzmäßigkeiten für die Parallelschaltung ableiten.
Merke: Bei der Parallelschaltung ist die Spannung an allen Widerständen gleich groß.
U1 = U2 = U3 = U
Rechnen Sie in der Schaltung Bild 4-14 nach!
I = I1 + I2 + I3 + ...
Merke: Der Gesamtstrom ist so groß wie die Summe der Einzelströme.
Teilt man in dieser Gleichung jeden Strom durch die immer gleiche Spannung U, erhält man
\[ \begin{aligned} \frac{I}{U} &= \frac{I_1}{U} + \frac{I_2}{U} + \frac{I_3}{U} + \ldots \\ \frac{I}{U} &= \frac{1}{R}; \ \frac{I_1}{U} = \frac{1}{R_1}; \ \frac{I_2}{U} = \frac{1}{R_2} \ \text{usw.} \end{aligned} \]
Dies führt zur Formel für die Berechnung des Ersatzwiderstandes einer Parallelschaltung. Man findet sie auch in der Formelsammlung der BNetzA (siehe Anhang 3 in diesem Buch).
\[ \frac{1}{R_G} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \ldots \frac{1}{R_n} \]In Worten ausgedrückt: Bei der Parallelschaltung ist der Kehrwert des Ersatzwiderstandes gleich der Summe der Kehrwerte der Einzelwiderstände. Man nennt den Kehrwert eines Widerstandes auch Leitwert.
Merke: Bei der Parallelschaltung ist der Gesamtleitwert gleich der Summe der Einzelleitwerte.
Der Quotient auf der rechten Seite der Formel bedeutet, dass diese Formel bis zur beliebigen Zahl n so weiter geht. Handelt es sich um drei parallel geschaltete Widerstände, endet der Index bei der Ziffer 3.
\[ \frac{1}{R_G} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \]Sind nur zwei Widerstände parallel geschaltet, lässt sich die Formel zur Berechnung des Gesamtwiderstandes auch anders schreiben. Können Sie in folgender Gleichung für die rechte Seite der Formel den Hauptnenner bilden und dann den Kehrwert dieses Ergebnisses schreiben?
\[ \frac{1}{R_G} = \frac{1}{R_1} + \frac{1}{R_2} \]Als Lösung muss herauskommen
\[ R_G = \frac{R_1 \cdot R_2}{R_1 + R_2} \]ehemalige Prüfungsfrage
| TD109 Zwei Widerstände von 20 Ω und 30 Ω sind parallel geschaltet. Wie groß ist der Ersatzwiderstand? | |
|---|---|
| 15 Ω | |
| 50 Ω | |
| 12 Ω | |
| 3,5 Ω | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TD110 Zwei Widerstände mit R1 = 100 Ω und R2 = 150 Ω sind parallel geschaltet. Wie groß ist der Ersatzwiderstand? | |
|---|---|
| 17,5 Ω | |
| 250 Ω | |
| 75 Ω | |
| 60 Ω | |
Schaltet man n gleiche Widerstände parallel, ergibt sich der Ersatzwiderstand, indem man den Einzelwert durch die Gesamtzahl n teilt.
\[ R= \frac{R_1}{n} \]Hat man beispielsweise fünf gleiche Widerstände von 100 Ohm parallel geschaltet, ist der Gesamtwiderstand ein Fünftel davon, also 20 Ohm.
Mit dieser Kenntnis lassen sich die vier Prüfungsaufgaben zu gemischten Schaltungen sehr leicht lösen.
Gemischte Schaltungen
In der Praxis hat man es oft mit gemischten Schaltungen aus teils in Reihe und teils parallel geschalteten Widerständen zu tun.
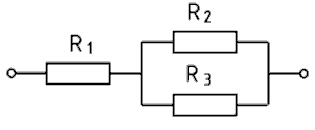
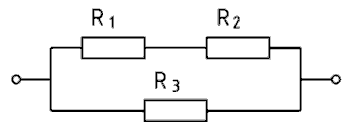
In der Grundschaltung Bild 4-15 links ist zu einer Parallelschaltung von R2 und R3 noch ein Widerstand R1 in Reihe geschaltet. In der Grundschaltung rechts ist zu der Reihenschaltung aus R1 und R2 ein Widerstand R3 parallel geschaltet. Entsprechend dieser Beschreibung erfolgt auch die Lösung zur Berechnung des Gesamtwiderstandes.
ehemalige Prüfungsfrage
| TD101 Wie groß ist der Ersatzwiderstand der Gesamtschaltung mit R1 = 500 Ω, R2 =1000 Ω, R3 = 1 kΩ? | |
|---|---|
 | |
| 5,1 kΩ | |
| 2,5 kΩ | |
| 501 Ω | |
| 1,0 kΩ | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TD102 Wie groß ist der Ersatzwiderstand der Gesamtschaltung? | |
|---|---|
Gegeben: R1 = 1 kΩ, R2 = 2000 Ω und R3 = 2 kΩ
 | |
| 501 Ω | |
| 2 kΩ | |
| 2,5 kΩ | |
| 5,1 kΩ | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TD103 Wie groß ist der Ersatzwiderstand der Gesamtschaltung? R1 = 500 Ω, R2 = 500 Ω und R3 = 1 kΩ | |
|---|---|
 | |
| 250 Ω | |
| 500 Ω | |
| 1 kΩ | |
| 2 kΩ | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TD104 Berechnen Sie den Ersatzwiderstand der Gesamtschaltung | |
|---|---|
 Gegeben: R1 = 500 Ω, R2 = 1,5 kΩ und R3 = 2 kΩ | |
| 500 Ω | |
| 1 kΩ | |
| 2 kΩ | |
| 4 kΩ | |
Lösungsweg (hier klicken zum Anzeigen):
Zusammenfassung
Reihenschaltung
- Der Strom ist überall gleich.
- Die Summe der Teilspannungen ist gleich der Gesamtspannung.
- Die Spannungen verhalten sich wie die zugehörigen Widerstände.
- Der Gesamtwiderstand ist gleich der Summe der Einzelwiderstände.
Parallelschaltung
- Die Spannung ist überall gleich.
- Die Summe der Teilströme ist gleich dem Gesamtstrom.
- Die Ströme verhalten sich umgekehrt wie die zugehörigen Widerstände
- Der Gesamtleitwert ist gleich der Summe der Einzelleitwerte.
- Der Gesamtwiderstand ist immer kleiner als der kleinste Einzelwiderstand.
Gemischte Schaltung
Bei einer gemischten Schaltung geht man so vor, dass man zunächst die Widerstände, die eindeutig parallel oder eindeutig in Reihe geschaltet sind, zu einem Ersatzwiderstand zusammenfasst und dann mit diesem Ersatzwiderstand weiter rechnet.
Viel Erfolg beim Lehrgang wünscht Ihnen Eckart Moltrecht DJ4UF!
| Copyright-Hinweis: | |
|---|---|
 | Dieser DARC-Online-Lehrgang wurde mit freundlicher Genehmigung des Autors Eckart K. W. Moltrecht aus seinen Büchern "Amateurfunk-Lehrgang für das Amateurfunkzeugnis" aus dem VTH-Verlag (möglicherweise einer älteren Auflage!) für das Internet umgewandelt. Das Copyright liegt beim Autor und beim Verlag. Mehr über den Autor! |
 | Die Darstellung auch nur von Auszügen oder Zeichnungen oder Fotos im Internet ist untersagt. Für die private Verwendung können Sie gern eine Genehmigung beim Autor erhalten. Schreiben Sie eine E-Mail an eckart.moltrecht(at)gmail.com! |
Letzte Bearbeitung: 24.05.2017 DJ4UF, 04.04.2020 DH8GHH
Fehlermeldungen mit Linkangabe an DH8GHH@darc.de

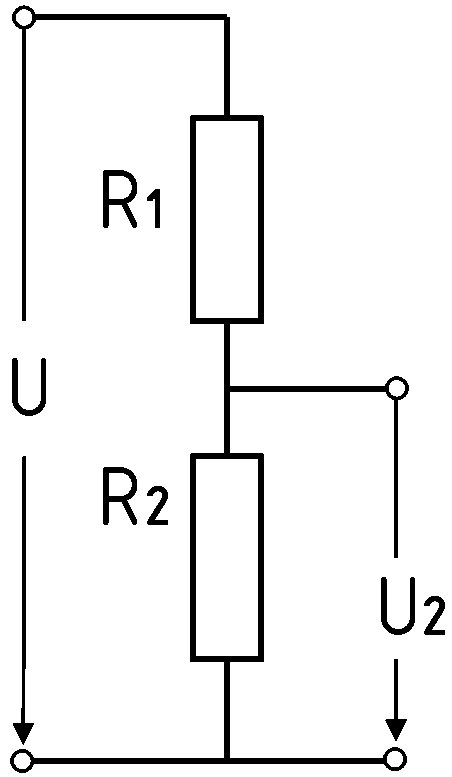 \(
\begin{aligned}
\frac{U_2}{U} &= \frac{R_2}{R} \\ \\
R &= R_1 + R_2 \\ \\
U_2 &= \frac{R_2}{R_1 + R_2}U \\ \\
U_2 &= \frac{2,2}{10 + 2,2} \cdot 12,2 \ \text{V} = \mathbf{2{,}2 \ V}
\end{aligned}
\)
\(
\begin{aligned}
\frac{U_2}{U} &= \frac{R_2}{R} \\ \\
R &= R_1 + R_2 \\ \\
U_2 &= \frac{R_2}{R_1 + R_2}U \\ \\
U_2 &= \frac{2,2}{10 + 2,2} \cdot 12,2 \ \text{V} = \mathbf{2{,}2 \ V}
\end{aligned}
\)