Neue Ausbildungsplattform für Klasse N
Das Ausbildungsmaterial für Klasse N findest du auf www.50Ohm.de
Hinweis: Dieser Lehrgang bezieht sich auf die alten Fragenkataloge, nach denen nur noch bis April 2024 geprüft wird.
Das aktuelle Ausbildungsmaterial, für Prüfungen ab Juni 2024 findest Du ebenfalls auf www.50Ohm.de
Kapitel 5: Kondensator
Nach dem Widerstand in den vorigen Kapiteln geht es um das zweitwichtigste Bauelement der Elektrotechnik: Der Kondensator.
Inhaltsübersicht
- Was ist ein Kondensator?
- Kapazität
- Parallelschaltung
- Reihenschaltung
- Gemischte Schaltungen
- Wechselstromwiderstand
- Bauformen
- Kennzeichnung
Was ist ein Kondensator?
In elektronischen Geräten, in Sendern und Empfängern, werden Sie an Bauelementen außer Widerständen recht häufig Kondensatoren finden.
Ein Kondensator besteht aus zwei voneinander isolierten, sich gegenüberstehenden Leitern (z.B. Metallflächen wie in Bild 5-2) und dem dazwischen liegenden Isolierstoff (Dielektrikum, sprich: Di-Elektrikum).
Kapazität
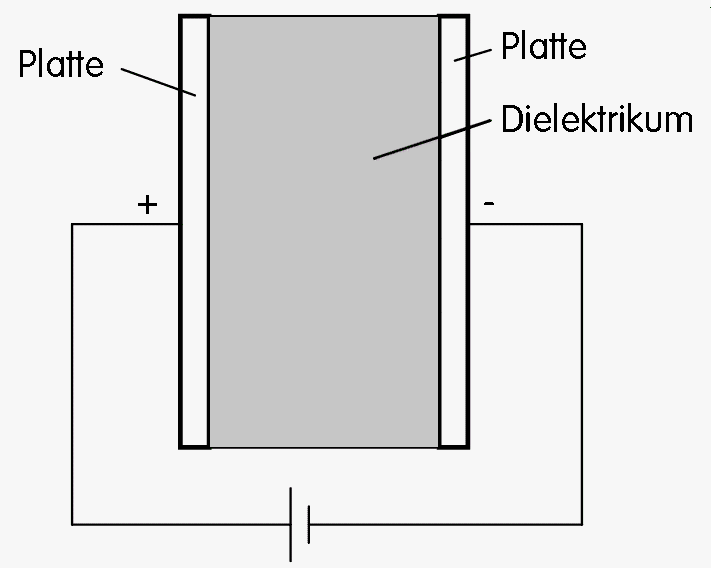
Legt man an die Platten eine elektrische Spannung, werden von der einen Platte Elektronen abgezogen und auf der anderen Platte Elektronen zugefügt. Entfernt man nun die Spannung als Ursache des elektrischen Feldes von den beiden Elektroden, bleibt der derzeitige Zustand erhalten, weil sich die Platten gegenseitig anziehen.
Es können also elektrische Ladungen auf den Platten eines Kondensators gespeichert werden. Dieses Speichervermögen bezeichnet man als KapazitätC .
Ein Kondensator vermag umso mehr elektrische Ladungen Q zu speichern, je größer seine Kapazität C und je höher die angelegte Spannung U ist.
Dies kann durch folgende Formel ausgedrückt werden.
Die Einheit der Kapazität ist das Farad F.
\[ 1 \ \text{F} = 1 \frac{\text{As}}{\text{V}} \]| 1 Mikrofarad | = | 1 µF | = | 10-6F | = | 1000 nF |
| 1 Nanofarad | = | 1 nF | = | 10-9F | = | 1000 pF |
| 1 Pikofarad | = | 1 pF | = | 10-12F |
Die Kapazität C hängt von der Fläche A der gegenüberliegenden leitenden Flächen und dem Abstand d zwischen diesen Flächen, sowie vom Werkstoff des Dielektrikums ab. Die Abhängigkeit vom Werkstoff wird in der Dielektrizitätszahl ε (griechisch: epsilon) ausgedrückt.
\[ \varepsilon = \varepsilon_0 \cdot \varepsilon_r \]Damit lässt sich die Kapazität eines Kondensators aus seinen geometrischen Abmessungen errechnen.
\[ C = \frac{\varepsilon_0 \cdot \varepsilon_r \cdot A}{d}\]Merke: Die Kapazität C eines Kondensators ist umso größer , je größer die Fläche A und je geringer der Abstand d der Platten ist. Die Einheit ist das Farad F.
ehemalige Prüfungsfrage
| TC201 Welche Aussage zur Kapazität eines Kondensators ist richtig? | |
|---|---|
| Je größer der Plattenabstand ist, desto kleiner ist die Kapazität. | |
| Je größer die angelegte Spannung ist, desto kleiner ist die Kapazität. | |
| Je größer die Plattenoberfläche ist, desto kleiner ist die Kapazität. | |
| Je größer die Dielektrizitätszahl ist, desto kleiner ist die Kapazität. | |
Lösungsweg (hier klicken zum Anzeigen):
Parallelschaltung von Kondensatoren
Wie bei Widerständen gibt es bei Kondensatoren eine Parallelschaltung, eine Reihenschaltung und die gemischte Schaltung.
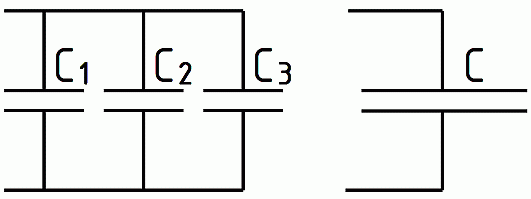
Bei der Parallelschaltung vergrößert sich die wirksame Fläche (Bild 5-3) der gegenüber stehenden Platten. Mit größerer Fläche
ergibt sich eine im Verhältnis größere Kapazität. Daraus lässt sich Folgendes ableiten.
Die Gesamtkapazität C bei der Parallelschaltung von Kondensatoren ist gleich der Summe der Einzelkapazitäten.
ehemalige Prüfungsfrage
| TC206 Drei Kondensatoren mit den Kapazitäten C1 = 0,1 µF, C2 = 150 nF und C3 = 50000 pF werden parallel geschaltet. Wie groß ist die Gesamtkapazität? | |
|---|---|
| 0,027 µF | |
| 0,255 µF | |
| 0,3 µF | |
| 2,73 nF | |
Lösungsweg (hier klicken zum Anzeigen):
Reihenschaltung von Kondensatoren
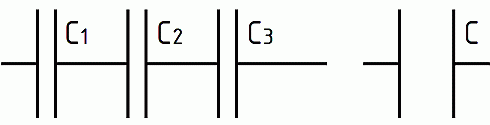
Die Reihenschaltung mehrerer Kondensatoren (Bild 5-4) entspricht einer Vergrößerung des Plattenabstandes, was wiederum eine Kapazitätsverminderung bedeutet. Die Gesamtkapazität ist bei einer Reihenschaltung kleiner als die kleinste Einzelkapazität.
\[ \frac{1}{C_G} = \frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}+... \]Entsprechend der Formel für die Parallelschaltung von zwei Widerständen kann für die Reihenschaltung von zwei Kondensatoren folgende Formel hergeleitet werden.
\[ C_G = \frac{C_1 \cdot C_2}{C_1 + C_2} \]Übungsaufgabe
| ÜB501 Zwei Kondensatoren von 100 pF und 150 pF sind hintereinander (in Serie) geschaltet. Berechnen Sie die Gesamtkapazität. |
|---|
Lösung mit der zweiten Formel
\[ C_G = \frac{100 \ \text{pF} \cdot 150 \ \text{pF}}{100 \ \text{pF} + 150 \ \text{pF}} = \frac{100 \ \text{pF} \cdot 150 \ \text{pF}}{250 \ \text{pF}} \]pF kürzt sich einmal heraus.
CG = 60 pF
Werden zwei gleich große Kondensatoren in Reihe geschaltet, halbiert sich die Kapazität, schaltet man drei gleiche Kondensatoren in Reihe, beträgt die Kapazität ein Drittel der eines Einzelkondensators und so weiter.
Gemischte Schaltungen
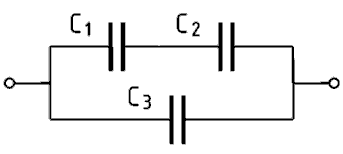
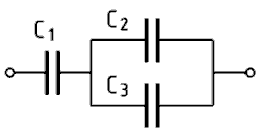
Wie bei Widerständen gibt es bei der gemischten Schaltung von insgesamt drei Kondensatoren die beiden Prinzipschaltungen: Zwei Kondensatoren parallel und dazu einer in Reihe oder zwei Kondensatoren in Reihe und dazu einer parallel, wie man dies in den beiden folgenden Prüfungsaufgaben sehen kann.
ehemalige Prüfungsfrage
| TD105 Berechnen Sie die Gesamtkapazität der gemischten Schaltung. | |
|---|---|
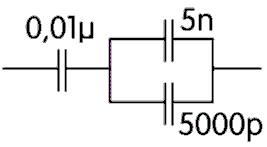 | |
| 0,015 nF | |
| 5 nF | |
| 7,5 nF | |
| 10 nF | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TD107 Welche Gesamtkapazität hat die folgende Schaltung? Gegeben: C1 = 0,01 µF; C2 = 10 nF; C3 = 5000 pF | |
|---|---|
 | |
| 2,5 nF | |
| 5 nF | |
| 10 nF | |
| 0,015 nF | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TD106 Welche Gesamtkapazität hat die folgende Schaltung?
Gegeben: C1 = 0,02 µF; C2 = 10 nF; C3 = 10000 pF | |
|---|---|
 | |
| 2,5 nF | |
| 5 nF | |
| 10 nF | |
| 40 nF | |
Wechselstromwiderstand
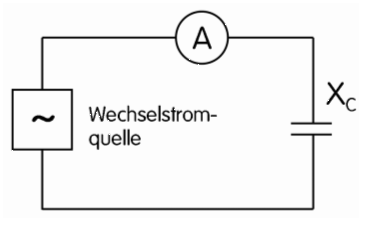
Ein Kondensator sperrt Gleichstrom.
Schließt man ihn aber an Wechselspannung (Bild 5-5), entspricht dies einer dauernden Ladung und Entladung des Kondensators. Je schneller die Wechsel sind, desto rascher erfolgt die Umladung. Dabei zeigt ein Strommesser, der in den Stromkreis geschaltet ist, einen Wechselstrom an, der sich aus Lade- und Entladestrom zusammensetzt.
Entsprechend dem Widerstand nach dem ohmschen Gesetz bezeichnet man das Verhältnis aus anliegender Spannung zum fließenden Wechselstrom als "Wechselstromwiderstand" des Kondensators XC.
\[ X_C = \frac{U_C}{I_C} \]Der Wechselstromwiderstand lässt sich auch aus Kapazität und Frequenz berechnen.
\[ X_C = \frac{1}{2 \cdot \pi \cdot f \cdot C} \]Aus dieser Formel erkennt man aber, dass der Wechselstromwiderstand umso kleiner wird, je höher Frequenz oder Kapazität sind. Also: Bei höherer Frequenz leitet ein Kondensator den Wechselstrom besser. Ein Kondensator größerer Kapazität leitet den Wechselstrom besser.
ehemalige Prüfungsfrage
| TC208 Mit zunehmender Frequenz | |
|---|---|
| steigt der Wechselstromwiderstand des Kondensators | |
| sinkt der Wechselstromwiderstand des Kondensators. | |
| steigt der Wechselstromwiderstand des Kondensators bis zu einem Maximum und sinkt dann wieder. | |
| sinkt der Wechselstromwiderstand des Kondensators bis zu einem Minimum und steigt dann wieder. | |
Bauformen von Kondensatoren

Kondensatoren bestehen immer aus zwei gegenüber liegenden leitenden Flächen mit einem Dielektrikum dazwischen. Häufig bestehen die leitenden Flächen aus Aluminiumfolie, die mit dem Dielektrikum beschichtet und das Ganze dann aufgewickelt wird. Das Dielektrikum muss einerseits gut isolieren, soll aber andererseits einen großen Dielektrizitätswert haben, um eine große Kapazität zu ermöglichen. Als Dielektrikum werden zum Teil keramische Werkstoffe oder auch Kunststoffe (zum Beispiel Styroflex) verwendet. Luft als Dielektrikum kommt bei den mechanisch veränderbaren (Plattendrehkondensatoren) vor.
Für sehr große Kapazitäten verwendet man Elektrolytkondensatoren. Bei diesen Kondensatoren besteht die eine "Platte" aus einer (lose aufgewickelten) angerauter Metallfolie und die andere aus einer elektrisch leitenden Flüssigkeit, dem Elektrolyt. Auf der Oberfläche der Metallfolie wird chemisch eine dünne Haut gebildet, die Strom nicht leitet. Sie ist das Dielektrikum dieses Kondensators. Weil sie sehr dünn und die Oberfläche der Metallfolie durch das Anrauen besonders groß ist, erreicht man hohe Kapazitäten.
Im Gegensatz zu den meisten anderen Kondensatoren sind Elektrolytkondensatoren nicht symmetrisch. Man sagt, sie sind gepolt. Auf einem solchen Kondensator sind die "+" und "-" -Anschlüsse markiert. Hält man sich nicht daran und schließt eine Gleichspannung andersherum an, so wird zunächst die dünne Haut zerstört: Der Kondensator wird leitend. Der nun fließende Strom zersetzt den Elektrolyten. Es entsteht ein Gas, das den Kondensator zum Platzen bringen kann.
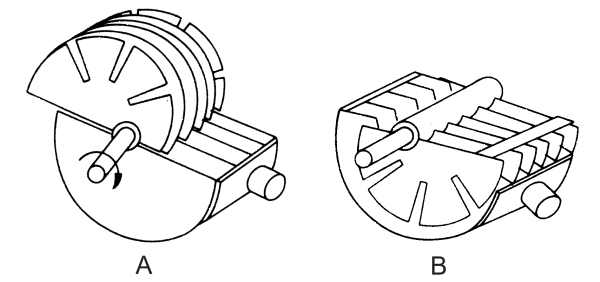
A: Platten herausgedreht, B: Platten eingedreht
Es gibt mechanisch veränderbare Kondensatoren, die aber aus Kostengründen mehr und mehr durch Kapazitätsdioden ersetzt werden. Im Bild 5-7 ist ein Drehkondensator dargestellt. Mit Hilfe einer Drehachse kann man den drehbaren Teil (Rotor) mehr oder weniger zwischen die Platten des feststehenden Teils (Stator) eindrehen und damit die Kapazität verändern.
Im Bild 5-8 sind die Schaltzeichen für Kondensatoren dargestellt. Veränderbare Kondensatoren erhalten wie veränderbare Widerstände einen Schrägstrich durch das Symbol. Ein Querstrich am Ende bedeutet, dass dieser Kondensator nur mit Hilfe eines Werkzeugs verändert werden kann (Trimmer). Ein Pfeil bedeutet Bedienbarkeit von außen. Gepolte Kondensatoren erhalten entweder ein Pluszeichen auf der entsprechenden Platte (d) oder werden einseitig dicker gezeichnet (e).
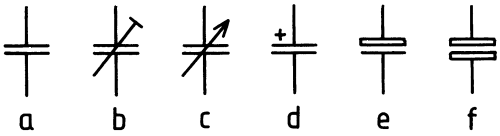
a allgemein, b einstellbar (Trimmer), c veränderbar, d gepolt, e Elko gepolt, f Elko ungepolt
Kennzeichnung von Kondensatoren
Früher hat man die Daten (Kapazität, Toleranz, maximale Spannung) auf den Kondensator aufgedruckt. Im Zuge der Miniaturisierung ist kein Platz mehr dafür, außer bei den noch immer großen Elektrolytkondensatoren (Bild 5-5). Deshalb verwendet man zur Kennzeichnung des Kapazitätswertes ein ähnliches System wie bei den SMD-Widerständen, nämlich die Größenkennzeichnung Milli (m), Mikro (µ), Nano (n) oder Piko (p) an die Stelle des Kommas zu setzen.
Beispiele
m47 = 0,47 mF = 470 µF
4µ7 = 4,7 µF
n47 = 0,47 nF = 470 pF
4n7 = 4,7 nF
4p7 = 4,7 pF
ehemalige Prüfungsfrage
| TC203 Welche Kapazität hat der folgend abgebildete Kondensator? | |
|---|---|
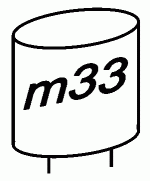 | |
| 3,3 µF | |
| 33 µF | |
| 330 µF | |
| 33000 µF | |
| TC202 Ein Bauelement, bei dem sich Platten auf einer keramisch isolierten Achse befinden, die zwischen fest stehende Platten hineingedreht werden können, nennt man | |
|---|---|
| Tauchkondensator | |
| Drehkondensator | |
| Keramischer Kondensator | |
| Rotorkondensator | |
ehemalige Prüfungsfrage
| TC207 Bei welchem der folgenden Bauformen von Kondensatoren muss beim Einbau auf die Polarität geachtet werden? | |
|---|---|
| Elektrolytkondensator | |
| Keramischer Kondensator | |
| Styroflexkondensator | |
| Plattenkondensator | |
| TC204 Die Kapazität eines Kondensators ist mit “n47” angegeben. Welcher Kapazität entspricht diese Angabe? | |
|---|---|
| 470 pF | |
| 4,7 pF | |
| 47 pF | |
| 4700 pF | |
ehemalige Prüfungsfrage
| TC205 Die Kapazität eines Kondensators ist mit " 8p2 " angegeben . Welcher Kapazität entspricht diese Angabe? | |
|---|---|
| 82 pF | |
| 0,82 pF | |
| 820 pF | |
| 8,2 pF | |
Viel Erfolg beim Lehrgang wünscht Ihnen Eckart Moltrecht DJ4UF!
| Copyright-Hinweis: | |
|---|---|
 | Dieser DARC-Online-Lehrgang wurde mit freundlicher Genehmigung des Autors Eckart K. W. Moltrecht aus seinen Büchern "Amateurfunk-Lehrgang für das Amateurfunkzeugnis" aus dem VTH-Verlag (möglicherweise einer älteren Auflage!) für das Internet umgewandelt. Das Copyright liegt beim Autor und beim Verlag. Mehr über den Autor! |
 | Die Darstellung auch nur von Auszügen oder Zeichnungen oder Fotos im Internet ist untersagt. Für die private Verwendung können Sie gern eine Genehmigung beim Autor erhalten. Schreiben Sie eine E-Mail an eckart.moltrecht(at)gmail.com! |
Letzte Bearbeitung: 24.05.2017 DJ4UF, 04.04.2020 DH8GHH
Fehlermeldungen mit Linkangabe an DH8GHH@darc.de






