Ein weiteres wichtiges Bauelement der Elektrotechnik ist die Spule.

Inhaltsübersicht

• Die Induktivität
• Bauformen von Spulen
• Reihen- und Parallelschaltung
• Der Wechselstromwiderstand
• Der Transformator

Im vorigen Kapitel wurde der Kondensator besprochen. Hier geht es um die Spule, die in ihrem Verhalten in vielen Fällen mit dem eines Kondensators verglichen werden kann.

Die Induktivität

Eine Spule besteht aus aufgewickeltem Draht.

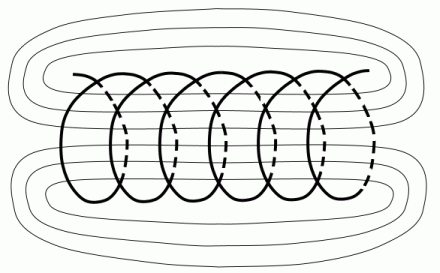
Wenn durch den Draht einer Spule Strom fließt, ist ein Magnetfeld vorhanden, das gespeicherte Energie darstellt. Das Magnetfeld ist nicht sichtbar. Wenn man mit einer Kompassnadel in die Nähe einer stromdurchflossenen Spule kommt und die Richtung der Nadel als Linie zeichnet, erhält man ein Bild ähnlich 6-1. Innerhalb der Spule verlaufen die Linien parallel. Man sagt, es handelt sich um ein homogenes Feld. Außerhalb schließen sich die Linien in Bögen.

ehemalige Prüfungsfrage

TB402  Wie nennt man das Feld im Innern einer langen Zylinderspule beim Fließen eines Gleichstroms?
	Homogenes elektrisches Feld
	Zentriertes magnetisches Feld
	Konzentrisches Magnetfeld
	Homogenes magnetisches Feld

Energieübertragung kann sehr schnell, aber niemals augenblicklich erfolgen. Sie dauert immer eine gewisse Zeit. Deshalb steigt der Strom in einer Spule nie augenblicklich an. Er baut sich immer nach und nach auf, während die Energie in das Magnetfeld übertragen wird. Dieses langsame Ansteigen soll durch einen Versuch nachgewiesen werden.

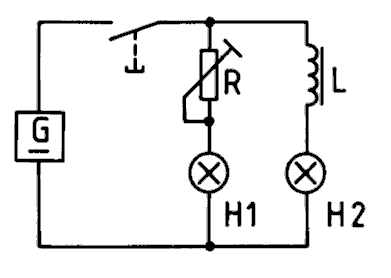
Schaltet man wie in Bild 6-2 zwei Glühlampen gleichzeitig an eine Spannungsquelle, wobei eine Glühlampe über einen Widerstand und die andere über eine Spule mit vielen Windungen und Eisenkern angeschlossen ist, so leuchtet die Lampe mit der Spule deutlich später auf, obwohl nachher beide Lampen gleich hell leuchten. Der Strom wird also verzögert.

Testen Sie sich, indem Sie in folgender Aufgabe links auf die Fragezeichen klicken, aber nur einmal in jeder Tabelle!

ehemalige Prüfungsfrage

TC305  Schaltet man zwei Glühlampen gleichzeitig an eine Spannungsquelle (Bild 6-2), wobei eine Glühlampe zum Helligkeitsausgleich über einen Widerstand und die andere über eine Spule mit vielen Windungen und Eisenkern angeschlossen ist, so
	leuchtet H1 zuerst.
	leuchtet H2 zuerst.
	leuchten H1 und H2 genau gleich schnell.
	leuchtet H2 kurz auf und geht wieder aus. H1 leuchtet.

Sie haben die Frage gut beantwortet, wenn Sie in der linken Spalte nur einmal das Wort "Richtig" sehen und keinmal "Falsch".

Diese Verzögerung kommt dadurch zustande, dass zunächst in dem Draht der Spule eine Gegenspannung erzeugt wird, sobald sich der Strom durch die Spule ändert und das Magnetfeld aufgebaut wird. Diese Gegenspannung wird Selbstinduktionsspannung genannt.

Wenn man bei der Spule Bild 6-2 den Eisenkern herauslässt oder die die Spule durch eine mit weniger Windungen ersetzt, wird die Verzögerung geringer. Diese Abhängigkeit wird zusammengefasst in dem Selbstinduktionskoeffizienten, der Induktivität L.

Mathematisch lässt sich dies mit Hilfe von Formeln ausdrücken. Die Induktivität lässt sich aus ihren geometrischen Abmessungen und den Werkstoffeigenschaften des verwendeten Kerns berechnen.

Induktivität     -   Zum Vergleich: Kapazität

$$\begin{align} L &= \frac{\mu \cdot A}{l} N^{2} & C &= \frac{\varepsilon \cdot A}{d} \end{align}$$

Die Werkstoffeigenschaften des Kerns werden durch die Permeabilität µ gekennzeichnet, ähnlich wie die Dielektrizitätskonstante beim Kondensator. A ist die Querschnittsfläche der Spule. Beim Kondensator war dies die Plattenfläche. l ist die Länge der magnetischen Feldlinien. Beim Kondensator war dies der Plattenabstand – dort mit d bezeichnet. Hinzugekommen ist die quadratische Abhängigkeit von der Windungszahl.

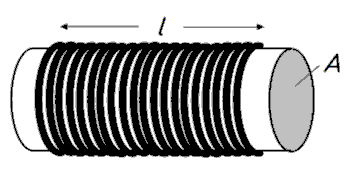
In der Praxis wird eine Spule so hergestellt, dass man den Draht Windung an Windung auf einen Wickelkörper wickelt, wie die Skizze im Bild 6-3 zeigt. Im Amateurfunk verwendet man auch selbst tragende Luftspulen aus dickem Draht (Bild 6-9).

Die Induktivität steigt mit dem Permeabilitätswert µ, mit der Querschnittsfläche A und sogar quadratisch mit der Windungszahl N , sinkt aber mit der Spulenlänge l.

Die Einheit der Induktivität ist Henry (H). Typisch sind Luftspulen in Mikrohenry (µH) oder Spulen mit Ferritkernen in Millihenry (mH).

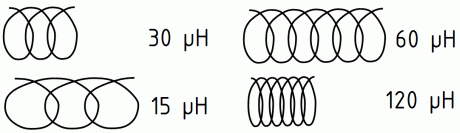
Wenn man eine Spule (zum Beispiel 30 µH) auf die doppelte Länge auseinander zieht, "verdünnt" sich das Magnetfeld und die Induktivität halbiert sich (15 µH). Wenn man eine Spule auf die halbe Länge zusammen staucht, ist das Magnetfeld konzentrierter: Die Induktivität der Spule hat sich verdoppelt. Wenn man eine Spule auf die doppelte Windungszahl verlängert, verdoppelt sich die Induktivität ebenfalls (60 µH). Wenn man die nun doppelt so lange Spule anschließend wieder auf die ursprüngliche Länge zusammenstaucht, verdoppelt sich die Induktivität nochmals (120 µH). Man hat also die vierfache Induktivität der ursprünglichen Spule.
Mit dieser Ableitung soll der quadratische Zusammenhang verdeutlicht werden. Merken Sie sich bitte nur: Verdoppelt man die Windungszahl bei sonst gleichen Abmessungen, vervierfacht sich die Induktivität einer Spule.

ehemalige Prüfungsfrage

TC301  Wie ändert sich die Induktivität einer Spule von 12 µH, wenn die Windungszahl bei gleicher Wickellänge verdoppelt wird?
	Die Induktivität steigt auf 48 µH.
	Die Induktivität steigt auf 24 µH.
	Die Induktivität sinkt auf 6 µH.
	Die Induktivität sinkt auf 3 µH.

Lösungsweg (hier klicken zum Anzeigen):

ehemalige Prüfungsfrage

TC302  Wie ändert sich die Induktivität einer Spule von 12 µH, wenn die Wicklung auf dem Wickelkörper bei gleicher Windungszahl auf den doppelten Wert auseinander gezogen wird?
	Die Induktivität sinkt auf 3 µH.
	Die Induktivität sinkt auf 6 µH.
	Die Induktivität steigt auf 24 µH.
	Die Induktivität steigt auf 48 µH.

Lösungsweg (hier klicken zum Anzeigen):

ehemalige Prüfungsfrage

TC303  Wie kann man die Induktivität einer Spule vergrößern?
	Durch Auseinanderziehen der Spule (Vergrößerung der Spulenlänge).
	Durch Einführen eines Kupferkerns in die Spule.
	Durch Stauchen der Spule (Verkürzen der Spulenlänge).
	Durch Einbau der Spule in einen Abschirmbecher.

Achtung! Ein Kupferkern wirkt wie eine Kurzschlusswindung und verringert die Induktivität.

Bauformen von Spulen

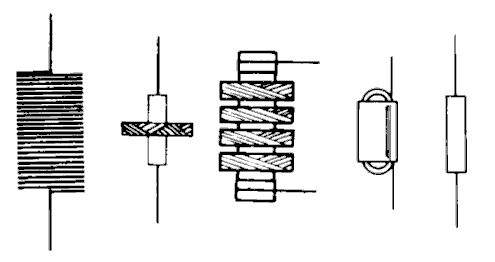
Fertig gewickelte Spulen kleiner Induktivität sind im Handel erhältlich. Luftspulen werden von Funkamateuren, die ihre Geräte selber bauen, selbst gewickelt.

Für die Selbstherstellung von Spulen gibt es Wickelkörper unterschiedlichster Bauformen, wovon einige im Bild 6-6 dargestellt sind.

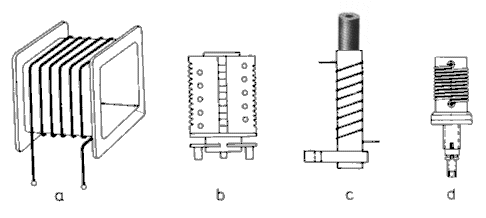
Um die Induktivität zu vergrößern, werden Spulenkerne (Bild 6-6c) aus Ferrit verwendet. Ferrit-Gewindekerne ermöglichen einstellbare Induktivitäten. Man kann diese Kerne unterschiedlich tief in die Spule hinein schrauben. Je nach dem, ob der Gewindekern sich hauptsächlich außerhalb der Spule befindet oder tief in sie hinein ragt, ist die Induktivität der Spule kleiner oder größer.

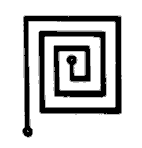
Im Amateurfunk-UHF-Bereich werden auch so genannte Printspulen verwendet. Sie werden wie bei gedruckten Leiterplatten in die Platine geätzt. Die Wicklungen sind meistens spiralförmig wie Bild 6-7 zeigt.

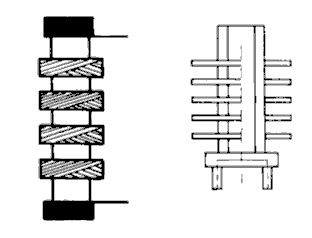
Um schädliche Kapazitäten zwischen den Drähten zu vermeiden, verwendet man Kreuzwickelspulen oder Spulenkörper, die in Kammern unterteilt sind.

Für Senderendstufen werden häufig Luftspulen aus dickerem Draht verwendet. Eine drehbare Spule mit Abgriff (Schleifer) ermöglicht die Variation der Induktivität.

Reihen- und Parallelschaltung von Spulen

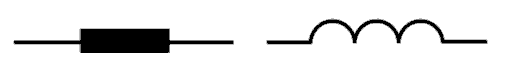
Nach DIN sind zwei Schaltzeichen zulässig, wobei das linke allgemein und das rechte Schaltzeichen vorwiegend bei Hochfrequenz angewendet wird (Bild 6-10).

Die Reihen- und die Parallelschaltung berechnet man wie beim Widerstand. Sind die Spulen in Reihe geschaltet, addieren sich die Induktivitäten der Spulen zur Gesamtinduktivität.

\[ L_G = L_1 + L_2 + \ldots \]

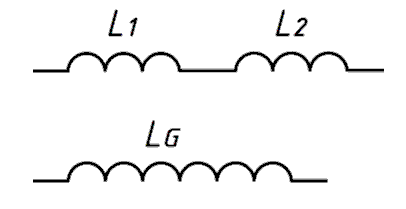
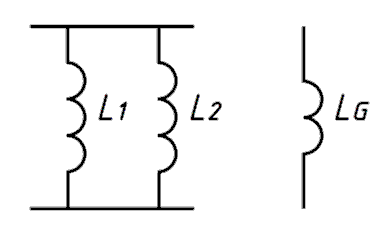
Entsprechend dem Widerstand lautet die Formel für die Parallelschaltung von Spulen

\[ \frac{1}{L_G} = \frac{1}{L_1}+\frac{1}{L_2} + \ldots \]

Die Berechnung einer reihen- oder einer Parallelschaltung von Induktivitäten kommt in der Prüfung nicht vor.

Der Wechselstromwiderstand

Schließt man eine Spule an Wechselspannung an (Bild 6-13), entspricht dies einer dauernden Änderung des Stromflusses, was eine ständige Entstehung einer Selbstinduktionsspannung und damit eine Verringerung des Stromflusses zur Folge hat. Dies wirkt sich also wie ein Widerstand aus. Man bezeichnet es, wie beim Kondensator, als Wechselstromwiderstand der Spule oder als induktiven Blindwiderstand X_L.

\[ X_L = \frac{U_L}{I_L} \]

Die Berechnung aus Induktivität und Frequenz erfolgt gemäß folgender Formel.

\[ X_L = 2 \cdot \pi \cdot f \cdot L \]

Vergleich mit Kondensator:

\[ X_C = \frac{1}{2 \cdot \pi \cdot f \cdot C} \]

Der Wechselstromwiderstand ist umso größer, je größer die Induktivität der Spule ist und je rascher sich der Strom ändert, je höher also die Frequenz des Wechselstroms ist. Beim Kondensator war es genau umgekehrt.

ehemalige Prüfungsfrage

TC306  Mit zunehmender Frequenz
	sinkt der Wechselstromwiderstand der Spule bis zu einem Minimum und steigt dann wieder.
	steigt der Wechselstromwiderstand der Spule bis zu einem Maximum und sinkt dann wieder.
	steigt der Wechselstromwiderstand der Spule.
	sinkt der Wechselstromwiderstand der Spule.

Transformator, Übertrager

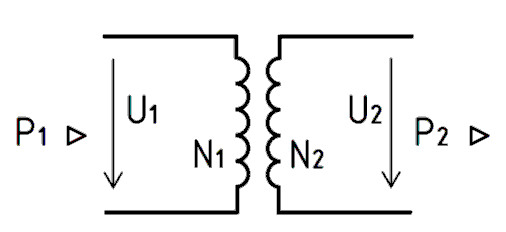
Werden zwei elektrisch getrennte Spulen von einem gemeinsamen Magnetfeld durchdrungen, zum Beispiel wenn sie auf einen gemeinsamen Kern gewickelt sind, verhalten sich die Wechselspannungen in den Wicklungen wie deren Windungszahlen. Das Verhältnis der Windungszahlen N₁ zu N₂ nennt man Übersetzungsverhältnis ü.

\[ ü = \frac{N_1}{N_2} = \frac{U_1}{U_2} \]

Die Eingangswicklung eines Übertragers nennt man Primärseite (N₁, U₁), die Ausgangswicklung Sekundärseite (N₂, U₂). Mit einem Übertrager lassen sich Spannungen, Ströme und auch ohmsche Widerstände "übersetzen" (transformieren).

ehemalige Prüfungsfrage

TC402  Ein Trafo liegt an 45 Volt und gibt 180 Volt ab. Seine Primärwicklung hat 150 Windungen. Wie groß ist seine Sekundärwindungszahl?
	46 Windungen
	30 Windungen
	600 Windungen
	850 Windungen

Lösungsweg (hier klicken zum Anzeigen):

ehemalige Prüfungsfrage

TC401  Ein Trafo liegt an 230 Volt und gibt 11,5 Volt ab. Seine Primärwicklung hat 600 Windungen. Wie groß ist seine Sekundärwindungszahl?
	20 Windungen
	30 Windungen
	52 Windungen
	180 Windungen

Lösungsweg (hier klicken zum Anzeigen):

ehemalige Prüfungsfrage

TC403  Die Primärspule eines Übertragers hat die fünffache Anzahl von Windungen der Sekundärspule. Wie hoch ist die erwartete Sekundärspannung, wenn die Primärspule an eine 230-V-Stromversorgung angeschlossen wird?
	9,2 Volt
	23 Volt
	46 Volt
	1150 Volt

Lösungsweg (hier klicken zum Anzeigen):

Viel Erfolg beim Lehrgang wünscht Ihnen Eckart Moltrecht DJ4UF!

Nach Oben

Zur Lehrgangs-Übersicht

Copyright-Hinweis:
	Dieser DARC-Online-Lehrgang wurde mit freundlicher Genehmigung des Autors Eckart K. W. Moltrecht aus seinen Büchern "Amateurfunk-Lehrgang für das Amateurfunkzeugnis" aus dem VTH-Verlag (möglicherweise einer älteren Auflage!) für das Internet umgewandelt. Das Copyright liegt beim Autor und beim Verlag. Mehr über den Autor!
	Die Darstellung auch nur von Auszügen oder Zeichnungen oder Fotos im Internet ist untersagt. Für die private Verwendung können Sie gern eine Genehmigung beim Autor erhalten. Schreiben Sie eine E-Mail an eckart.moltrecht(at)gmail.com!

Letzte Bearbeitungen: 25.05.2017 DJ4UF, 04.04.2020 DH8GHH
Fehlermeldungen mit Linkangabe bitte an DH8GHH@darc.de, insbesondere, wenn Sie mit einem Smartphone arbeiten!